A
MAZE
IN
ZAZAZA ENTER ZAZAZA
ZAZAZAZAZAZAZAAZAZAZAZAZAZAZ
ZAZAZAZAZAZAZAZAZAAZAZAZAZAZAZAZAZAZ
THE
MAGIKALALPHABET
ABCDEFGHIJKLMNOPQRSTUVWXYZZYXWVUTSRQPONMLKJIHGFEDCBA
12345678910111213141516171819202122232425262625242322212019181716151413121110987654321
WORK DAYS OF GOD
Herbert W Morris D.D.circa 1883
Page 22
"As all the words in the English language are composed out of the twenty-six letters of the alphabet,.."
LIGHT AND LIFE
Lars Olof Bjorn 1976
Page 197
"By writing the 26 letters of the alphabet in a certain order one may put down almost any message (this book 'is written with the same letters' as the Encyclopaedia Britannica and Winnie the Pooh, only the order of the letters differs). In the same way Nature is able to convey with her language how a cell and a whole organism is to be constructed and how it is to function. Nature has succeeded better than we humans; for the genetic code there is only one universal language which is the same in a man, a bean plant and a bacterium."
"BY WRITING THE 26 LETTERS OF THE ALPHABET IN A CERTAIN ORDER
ONE MAY PUT DOWN ALMOST ANY MESSAGE"
A |
B |
C |
D |
E |
F |
G |
H |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
1+0 |
1+1 |
1+2 |
1+3 |
1+4 |
1+5 |
1+6 |
1+7 |
1+8 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
S |
T |
U |
V |
W |
X |
Y |
Z |
I |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
9 |
1+9 |
2+0 |
2+1 |
2+2 |
2+3 |
2+4 |
2+5 |
2+6 |
ME |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
I |
ME |
I |
ME |
I |
ME |
I |
ME |
I |
9 |
18 |
9 |
18 |
9 |
18 |
9 |
18 |
9 |
= |
1+8 |
= |
1+8 |
= |
1+8 |
= |
1+8 |
= |
= |
9 |
= |
9 |
= |
9 |
= |
9 |
= |
I |
ME |
I |
ME |
I |
ME |
I |
ME |
1 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
I |
ME |
I |
ME |
I |
ME |
I |
ME |
1 |
"BY WRITING THE 26 LETTERS OF THE ALPHABET IN A CERTAIN ORDER
ONE MAY PUT DOWN ALMOST ANY MESSAGE"
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
= |
= |
= |
= |
= |
= |
= |
= |
= |
1+0 |
1+1 |
1+2 |
1+3 |
1+4 |
1+5 |
1+6 |
1+7 |
1+8 |
1+9 |
2+0 |
2+1 |
2+2 |
2+3 |
2+4 |
2+5 |
2+6 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
A |
B |
C |
D |
E |
F |
G |
H |
|
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A
HISTORY OF GOD
Karen Armstrong
The God of the Mystics
Page 250
"(The Book of Creation). There is no attempt to describe the creative process realistically; the account is unashamedly symbolic and shows God creating the world by means of language as though he were writing a book. But language has been entirely transformed and the message of creation is no longer clear. Each letter of the Hebrew alphabet is given a numerical value; by combining the letters with the sacred numbers, rearranging them in endless configurations, the mystic weaned his mind away from the normal connotations of words."
A |
B |
C |
D |
E |
F |
G |
H |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
1+0 |
1+1 |
1+2 |
1+3 |
1+4 |
1+5 |
1+6 |
1+7 |
1+8 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
S |
T |
U |
V |
W |
X |
Y |
Z |
I |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
9 |
1+9 |
2+0 |
2+1 |
2+2 |
2+3 |
2+4 |
2+5 |
2+6 |
ME |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
I |
ME |
I |
ME |
I |
ME |
I |
ME |
I |
9 |
18 |
9 |
18 |
9 |
18 |
9 |
18 |
9 |
= |
1+8 |
= |
1+8 |
= |
1+8 |
= |
1+8 |
= |
= |
9 |
= |
9 |
= |
9 |
= |
9 |
= |
I |
ME |
I |
ME |
I |
ME |
I |
ME |
1 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
I |
ME |
I |
ME |
I |
ME |
I |
ME |
1 |
THERE IS NO ATTEMPT MADE TO DESCRIBE THE CREATIVE PROCESS REALISTICALLY
THE ACCOUNT IS SYMBOLIC AND SHOWS GOD CREATING THE WORLD BY MEANS OF LANGUAGE
AS THOUGH WRITING A BOOK BUT LANGUAGE ENTIRELY TRANSFORMED
THE MESSAGE OF CREATION IS CLEAR EACH LETTER OF
THE
ALPHABET
IS
GIVEN
A
NUMERICAL
VALUE BY COMBINING THE LETTERS WITH THE SACRED NUMBERS
REARRANGING THEM IN ENDLESS CONFIGURATIONS
THE MYSTIC WEANED THE MIND AWAY FROM THE NORMAL CONNOTATIONS OF WORDS
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
1+0 |
1+1 |
1+2 |
1+3 |
1+4 |
1+5 |
1+6 |
1+7 |
1+8 |
1+9 |
2+0 |
2+1 |
2+2 |
2+3 |
2+4 |
2+5 |
2+6 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
A |
B |
C |
D |
E |
F |
G |
H |
|
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
FINGERPRINTS OF THE GODS
A QUEST FOR THE BEGINNING AND THE END
Graham Hancock 1995
Chapter 32
Speaking to the Unborn
Page 285
"It is understandable that a huge range of myths from all over the ancient world should describe geological catastrophes in graphic detail. Mankind survived the horror of the last Ice Age, and the most plausible source for our enduring traditions of flooding and freezing, massive volcanism and devastating earthquakes is in the tumultuous upheavals unleashed during the great meltdown of 15,000 to 8000 BC. The final retreat of the ice sheets, and the consequent 300-400 foot rise in global sea levels, took place only a few thousand years before the beginning of the historical period. It is therefore not surprising that all our early civilizations should have retained vivid memories of the vast cataclysms that had terrified their forefathers.
Much harder to explain is the peculiar but distinctive way the myths of cataclysm seem to bear the intelligent imprint of a guiding hand.l Indeed the degree of convergence between such ancient stories is frequently remarkable enough to raise the suspicion that they must all have been 'written' by the same 'author'.
Could that author have had anything to do with the wondrous deity, or superhuman, spoken of in so many of the myths we have reviewed, who appears immediately after the world has been shattered by a horrifying geological catastrophe and brings comfort and the gifts of civilization to the shocked and demoralized survivors?
White and bearded, Osiris is the Egyptian manifestation of this / Page 286 /
universal figure, and it may not be an accident that one of the first acts he is remembered for in myth is the abolition of cannibalism among the primitive inhabitants of the Nile Valley.2 Viracocha, in South America, was said to have begun his civilizing mission immediately after a great flood; Quetzalcoatl, the discoverer of maize, brought the benefits of crops, mathematics, astronomy and a refined culture to Mexico after the Fourth Sun had been overwhelmed by a destroying deluge.
Could these strange myths contain a record of encounters between scattered palaeolithic tribes which survived the last Ice Age and an as yet unidentified high civilization which passed through the same epoch?
And could the myths be attempts to communicate?
A message in the bottle of time"
'Of all the other stupendous inventions,' Galileo once remarked,
what sublimity of mind must have been his who conceived how to communicate his most secret thoughts to any other person, though very distant either in time or place, speaking with those who are in the Indies, speaking to those who are not yet born, nor shall be this thousand or ten thousand years? And with no greater difficulty than the various arrangements of two dozen little signs on paper? Let this be the seal of all the admirable inventions of men.3
If the 'precessional message' identified by scholars like Santillana, von Dechend and Jane Sellers is indeed a deliberate attempt at communication by some lost civilization of antiquity, how come it wasn't just written down and left for us to find? Wouldn't that have been easier than encoding it in myths? Perhaps.
Nevertheless, suppose that whatever the message was written on got destroyed or worn away after many thousands of years? Or suppose that the language in which it was inscribed was later forgotten utterly (like the enigmatic Indus Valley script, which has been studied closely for more than half a century but has so far resisted all attempts at decoding)? It must be obvious that in such circumstances a written / Page 287 / legacy to the future would be of no value at all, because nobody would be able to make sense of it.
What one would look for, therefore, would be a universal language, the kind of language that would be comprehensible to any technologically advanced society in any epoch, even a thousand or ten thousand years into the future. Such languages are few and far between, but mathematics is one of them - and the city of Teotihuacan may be the calling-card of a lost civilization written in the eternal language of mathematics.
Geodetic data, related to the exact positioning of fixed geographical points and to the shape and size of the earth, would also remain valid and recognizable for tens of thousands of years, and might be most conveniently expressed by means of cartography (or in the construction of giant geodetic monuments like the Great Pyramid of Egypt, as
we shall see).
Another 'constant' in our solar system is the language of time: the great but regular intervals of time calibrated by the inch-worm creep of precessional motion. Now, or ten thousand years in the future, a message that prints out numbers like 72 or 2160 or 4320 or 25,920 should be instantly intelligible to any civilization that has evolved a modest talent for mathematics and the ability to detect and measure the almost imperceptible reverse wobble that the sun appears to make along the ecliptic against the background of the fixed stars..."
"What one would look for, therefore, would be a universal language, the kind of language that would be comprehensible to any technologically advanced society in any epoch, even a thousand or ten thousand years into the future. Such languages are few and far between, but mathematics is one of them"
"WRITTEN IN THE ETERNAL LANGUAGE OF MATHEMATICS"
W |
= |
5 |
- |
4 |
WHAT |
52 |
16 |
7 |
O |
= |
6 |
- |
3 |
ONE |
34 |
16 |
7 |
W |
= |
5 |
- |
5 |
WOULD |
75 |
21 |
3 |
L |
= |
3 |
- |
4 |
LOOK |
53 |
17 |
8 |
F |
= |
6 |
- |
3 |
FOR |
30 |
21 |
3 |
T |
= |
2 |
- |
9 |
THEREFORE |
100 |
46 |
1 |
W |
= |
5 |
- |
5 |
WOULD |
75 |
21 |
3 |
B |
= |
2 |
- |
2 |
BE |
7 |
7 |
7 |
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
U |
= |
3 |
- |
9 |
UNIVERSAL |
121 |
40 |
4 |
L |
= |
3 |
- |
8 |
LANGUAGE |
68 |
32 |
5 |
- |
- |
42 |
|
56 |
First Total |
|
|
|
- |
- |
4+2 |
- |
5+6 |
Add to Reduce |
6+1+6 |
2+3+8 |
4+9 |
- |
- |
6 |
- |
|
Second Total |
|
|
|
- |
- |
- |
- |
1+1 |
Reduce to Deduce |
1+3 |
1+3 |
1+3 |
- |
- |
|
- |
|
Essence of Number |
|
|
|
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
K |
= |
2 |
- |
4 |
KIND |
38 |
20 |
2 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
L |
= |
3 |
- |
8 |
LANGUAGE |
68 |
32 |
5 |
T |
= |
2 |
- |
4 |
THAT |
49 |
13 |
4 |
W |
= |
5 |
- |
5 |
WOULD |
75 |
21 |
3 |
B |
= |
2 |
- |
2 |
BE |
7 |
7 |
7 |
C |
= |
3 |
- |
14 |
COMPREHENSIBLE |
144 |
72 |
9 |
T |
= |
2 |
- |
2 |
TO |
35 |
8 |
8 |
A |
= |
1 |
- |
3 |
ANY |
40 |
13 |
4 |
T |
= |
2 |
- |
15 |
TECHNOLOGICALLY |
161 |
71 |
8 |
A |
= |
1 |
- |
2 |
ADVANCED |
54 |
27 |
9 |
S |
= |
1 |
- |
7 |
SOCIETY |
96 |
33 |
6 |
I |
= |
9 |
- |
2 |
IN |
23 |
14 |
5 |
A |
= |
1 |
- |
3 |
ANY |
40 |
13 |
4 |
E |
= |
5 |
- |
5 |
EPOCH |
48 |
29 |
2 |
- |
- |
47 |
|
87 |
First Total |
|
|
|
- |
- |
4+7 |
- |
8+7 |
Add to Reduce |
9+3+1 |
4+0+0 |
8+5 |
- |
- |
11 |
- |
|
Second Total |
|
|
|
- |
- |
1+1 |
- |
1+5 |
Reduce to Deduce |
1+3 |
- |
1+3 |
- |
- |
|
- |
|
Essence of Number |
|
|
|
S |
= |
1 |
- |
4 |
SUCH |
51 |
15 |
6 |
L |
= |
3 |
- |
9 |
LANGUAGES |
87 |
33 |
6 |
A |
= |
1 |
- |
3 |
ARE |
24 |
15 |
6 |
F |
= |
6 |
- |
3 |
FEW |
34 |
16 |
7 |
A |
= |
1 |
- |
3 |
AND |
19 |
10 |
1 |
F |
= |
6 |
- |
3 |
FAR |
25 |
16 |
7 |
B |
= |
2 |
- |
7 |
BETWEEN |
74 |
29 |
2 |
B |
= |
2 |
- |
3 |
BUT |
43 |
7 |
7 |
M |
= |
4 |
- |
11 |
MATHEMATICS |
112 |
40 |
4 |
I |
= |
9 |
- |
2 |
IS |
28 |
10 |
1 |
O |
= |
6 |
- |
3 |
ONE |
34 |
16 |
7 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
T |
= |
2 |
- |
4 |
THEM |
46 |
19 |
1 |
- |
- |
49 |
|
57 |
First Total |
|
|
|
- |
- |
4+9 |
- |
5+7 |
Add to Reduce |
5+9+8 |
2+3+8 |
5+8 |
- |
- |
11 |
- |
|
Second Total |
|
|
|
- |
- |
1+2 |
- |
1+2 |
Reduce to Deduce |
2+2 |
1+3 |
1+3 |
- |
- |
|
- |
|
Essence of Number |
|
|
|
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
L |
= |
3 |
- |
8 |
LANGUAGE |
68 |
32 |
5 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
L |
= |
3 |
- |
7 |
LETTERS |
99 |
27 |
9 |
A |
= |
1 |
- |
3 |
AND |
19 |
10 |
1 |
N |
= |
5 |
- |
7 |
NUMBERS |
73 |
28 |
1 |
- |
- |
19 |
|
28 |
First Total |
|
|
|
- |
- |
1+9 |
- |
2+8 |
Add to Reduce |
2+9+9 |
1+1+0 |
2+0 |
- |
- |
10 |
- |
|
Second Total |
|
|
|
- |
- |
1+0 |
- |
1+0 |
Reduce to Deduce |
2+0 |
- |
- |
- |
- |
|
- |
|
Essence of Number |
|
|
|
W |
= |
5 |
- |
4 |
WHAT |
52 |
16 |
7 |
O |
= |
6 |
- |
3 |
ONE |
34 |
16 |
7 |
W |
= |
5 |
- |
5 |
WOULD |
75 |
21 |
3 |
L |
= |
3 |
- |
4 |
LOOK |
53 |
17 |
8 |
F |
= |
6 |
- |
3 |
FOR |
30 |
21 |
3 |
T |
= |
2 |
- |
9 |
THEREFORE |
100 |
46 |
1 |
W |
= |
5 |
- |
5 |
WOULD |
75 |
21 |
3 |
B |
= |
2 |
- |
2 |
BE |
7 |
7 |
7 |
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
U |
= |
3 |
- |
9 |
UNIVERSAL |
121 |
40 |
4 |
L |
= |
3 |
- |
8 |
LANGUAGE |
68 |
32 |
5 |
T |
= |
2 |
- |
3 |
THE |
33 |
15 |
6 |
K |
= |
2 |
- |
4 |
KIND |
38 |
20 |
2 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
L |
= |
3 |
- |
8 |
LANGUAGE |
68 |
32 |
5 |
C |
= |
3 |
- |
4 |
THAT |
144 |
72 |
9 |
T |
= |
2 |
- |
5 |
WOULD |
35 |
8 |
8 |
A |
= |
1 |
- |
2 |
BE |
40 |
13 |
4 |
T |
= |
2 |
- |
14 |
COMPREHENSIBLE |
161 |
71 |
8 |
A |
= |
1 |
- |
2 |
TO |
54 |
27 |
9 |
S |
= |
1 |
- |
3 |
ANY |
96 |
33 |
6 |
I |
= |
9 |
- |
15 |
TECHNOLOGICALLY |
23 |
14 |
5 |
A |
= |
1 |
- |
2 |
ADVANCED |
40 |
13 |
4 |
E |
= |
5 |
- |
7 |
SOCIETY |
48 |
29 |
2 |
T |
= |
2 |
- |
2 |
IN |
49 |
13 |
4 |
W |
= |
5 |
- |
3 |
ANY |
75 |
21 |
3 |
B |
= |
2 |
- |
5 |
EPOCH |
7 |
7 |
7 |
S |
= |
1 |
- |
4 |
SUCH |
51 |
15 |
6 |
L |
= |
3 |
- |
9 |
LANGUAGES |
87 |
33 |
6 |
A |
= |
1 |
- |
3 |
ARE |
24 |
15 |
6 |
F |
= |
6 |
- |
3 |
FEW |
34 |
16 |
7 |
A |
= |
1 |
- |
3 |
AND |
19 |
10 |
1 |
F |
= |
6 |
- |
3 |
FAR |
25 |
16 |
7 |
B |
= |
2 |
- |
7 |
BETWEEN |
74 |
29 |
2 |
B |
= |
2 |
- |
3 |
BUT |
43 |
7 |
7 |
M |
= |
4 |
- |
11 |
MATHEMATICS |
112 |
40 |
4 |
I |
= |
9 |
- |
2 |
IS |
28 |
10 |
1 |
O |
= |
6 |
- |
3 |
ONE |
34 |
16 |
7 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
T |
= |
2 |
- |
4 |
THEM |
46 |
19 |
1 |
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
L |
= |
3 |
- |
8 |
LANGUAGE |
68 |
32 |
5 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
L |
= |
3 |
- |
7 |
LETTERS |
99 |
27 |
9 |
A |
= |
1 |
- |
3 |
AND |
19 |
10 |
1 |
N |
= |
5 |
- |
7 |
NUMBERS |
73 |
28 |
1 |
- |
- |
157 |
|
228 |
First Total |
|
|
|
- |
- |
1+5+7 |
- |
2+2+8 |
Add to Reduce |
2+4+4+4 |
9+8+6 |
2+1+2 |
- |
- |
13 |
- |
|
Second Total |
|
|
|
- |
- |
1+3 |
- |
1+2 |
Reduce to Deduce |
1+4 |
2+3 |
- |
- |
- |
|
- |
|
Essence of Number |
|
|
|
MATHEMATICS A LANGUAGE
OF
LETTER AND NUMBER
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
L |
= |
3 |
- |
8 |
LANGUAGE |
68 |
32 |
5 |
O |
= |
6 |
- |
2 |
OF |
21 |
12 |
3 |
L |
= |
3 |
- |
6 |
LETTER |
80 |
26 |
8 |
A |
= |
1 |
- |
3 |
AND |
19 |
10 |
1 |
N |
= |
5 |
- |
6 |
NUMBER |
73 |
28 |
1 |
S |
- |
19 |
|
26 |
First Total |
|
|
|
- |
- |
1+9 |
- |
2+6 |
Add to Reduce |
2+6+1 |
1+0+8 |
1+8 |
- |
- |
|
- |
|
Second Total |
|
|
|
- |
- |
1+0 |
- |
- |
Reduce to Deduce |
- |
- |
- |
- |
- |
1 |
- |
|
Essence of Number |
|
|
|


A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
1+0 |
1+1 |
1+2 |
1+3 |
1+4 |
1+5 |
1+6 |
1+7 |
1+8 |
1+9 |
2+0 |
2+1 |
2+2 |
2+3 |
2+4 |
2+5 |
2+6 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
A |
B |
C |
D |
E |
F |
G |
H |
|
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |




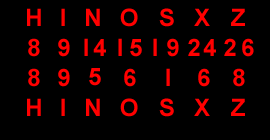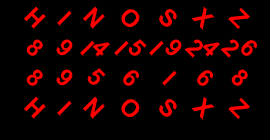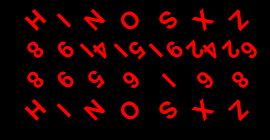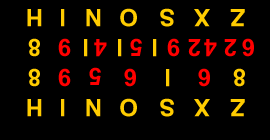

A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
1+0 |
1+1 |
1+2 |
1+3 |
1+4 |
1+5 |
1+6 |
1+7 |
1+8 |
1+9 |
2+0 |
2+1 |
2+2 |
2+3 |
2+4 |
2+5 |
2+6 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
A |
B |
C |
D |
E |
F |
G |
H |
|
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
|
|
|
S |
|
|
|
|
|
|
1 |
- |
1 |
- |
1 |
|
|
|
- |
|
|
A |
|
|
|
S |
|
|
|
|
|
|
- |
- |
- |
- |
- |
|
|
|
- |
|
|
B |
|
|
|
T |
|
|
|
|
|
|
2 |
- |
2 |
- |
2 |
|
|
|
- |
|
|
B |
|
|
|
T |
|
|
|
|
|
|
- |
- |
- |
- |
- |
|
|
|
- |
|
|
C |
|
|
|
U |
|
|
|
|
|
|
3 |
- |
3 |
- |
3 |
|
|
|
- |
|
|
C |
|
|
|
U |
|
|
|
|
|
|
- |
- |
- |
- |
- |
|
|
|
- |
|
|
D |
|
|
|
V |
|
|
|
|
|
|
4 |
- |
4 |
- |
4 |
|
|
|
1+2 |
|
|
D |
|
|
|
V |
|
|
|
|
|
|
- |
- |
- |
- |
- |
|
|
|
- |
|
|
E |
|
|
|
W |
|
|
|
|
|
|
5 |
- |
5 |
- |
5 |
|
|
|
1+5 |
|
|
E |
|
|
|
W |
|
|
|
|
|
|
- |
- |
- |
- |
- |
|
|
|
- |
|
|
F |
|
|
|
X |
|
|
|
|
|
|
6 |
- |
6 |
- |
6 |
|
|
|
1+8 |
|
|
F |
|
|
|
X |
|
|
|
|
|
|
- |
- |
- |
- |
- |
|
|
|
- |
|
|
G |
|
|
|
Y |
|
|
|
|
|
|
7 |
- |
7 |
- |
7 |
|
|
|
2+1 |
|
|
G |
|
|
|
Y |
|
|
|
|
|
|
- |
- |
- |
- |
- |
|
|
|
- |
|
|
H |
|
|
|
Z |
|
|
|
|
|
|
8 |
- |
8 |
- |
8 |
|
|
|
2+4 |
|
|
H |
|
|
|
Z |
|
|
|
|
|
|
- |
- |
- |
- |
- |
|
|
|
- |
|
|
I |
|
|
|
- |
|
|
|
|
|
|
9 |
- |
9 |
- |
- |
|
|
|
1+8 |
|
|
I |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
- |
|
|
1+2+6 |
|
|
5+4 |
|
|
|
|
|
|
|
|
|
|
|
THE
FAR YONDER SCRIBE
AND OFT TIMES SHADOWED SUBSTANCES WATCHED IN SOME AMAZE
THE
ZED ALIZ ZED
IN
SWIFT REPEAT SCATTER STAR DUST AMONGST THE LETTERS OF THEIR PROGRESS

NUMBER
9
THE SEARCH FOR THE SIGMA CODE
Cecil Balmond 1998
Cycles and Patterns
Page 165
Patterns
"The essence of mathematics is to look for patterns.
Our minds seem to be organised to search for relationships and sequences. We look for hidden orders.
These intuitions seem to be more important than the facts themselves, for there is always the thrill at finding something, a pattern, it is a discovery - what was unknown is now revealed. Imagine looking up at the stars and finding the zodiac!
Searching out patterns is a pure delight.
Suddenly the counters fall into place and a connection is found, not necessarily a geometric one, but a relationship between numbers, pictures of the mind, that were not obvious before. There is that excitement of finding order in something that was otherwise hidden.
And there is the knowledge that a huge unseen world lurks behind the facades we see of the numbers themselves."
- |
MATHEMATICS |
- |
- |
- |
4 |
MATH |
42 |
15 |
|
2 |
|
18 |
9 |
|
2 |
AT |
21 |
3 |
|
1 |
|
9 |
9 |
|
2 |
CS |
22 |
4 |
|
|
MATHEMATICS |
|
|
|
|
- |
1+1+2 |
4+0 |
3+1 |
|
MATHEMATICS |
|
|
|
11 |
CONDOLEEZZA |
126 |
54 |
9 |
4 |
RICE |
35 |
26 |
8 |
15 |
Add to Reduce |
|
|
|
1+5 |
Reduce to Deduce |
1+6+1 |
8+0 |
- |
|
Essence of Number |
|
|
|
15 |
CONDOLEEZZA RICE |
- |
- |
- |
|
C+O |
18 |
9 |
|
|
N+D |
18 |
9 |
|
|
O+L |
18 |
9 |
|
|
E+E+Z |
36 |
18 |
|
|
Z+A |
27 |
9 |
|
|
R |
18 |
9 |
|
|
I |
9 |
9 |
|
|
C+E |
8 |
8 |
|
15 |
CONDOLEEZA RICE |
- |
- |
- |
MACBETH
William Shakespeare
Circa 1564 - 1616
Act 1 Scene 3
First Witch
I myself have all the other,
And the very ports they blow,
All the quarters that they know
I' the shipman's card.
I will drain him dry as hay:
Sleep shall neither night nor day
Hang upon his pent-house lid;
He shall live a man forbid:
Weary se'nnights nine times nine
Shall he dwindle, peak and pine:
Though his bark cannot be lost,
Yet it shall be tempest-tost.
Look what I have.
ALL
The weird sisters, hand in hand,
Posters of the sea and land,
Thus do go about, about:
Thrice to thine and thrice to mine
And thrice again, to make up nine.
Peace! the charm's wound up.
- |
6 |
|
|
|
|
|
|
|
|
|
- |
|
|
|
- |
- |
|
- |
|
- |
8 |
- |
9 |
- |
- |
|
|
|
1+7 |
= |
|
= |
|
|
|
- |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
|
- |
|
2 |
= |
9 |
= |
3 |
5 |
|
|
|
1+9 |
= |
|
1+0 |
|
|
|
- |
|
20 |
- |
18 |
- |
3 |
5 |
|
|
|
4+6 |
= |
|
1+0 |
|
|
|
- |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
|
20 |
8 |
18 |
9 |
3 |
5 |
|
|
|
6+3 |
= |
|
= |
|
|
|
- |
|
2 |
8 |
9 |
9 |
3 |
5 |
|
|
|
3+6 |
= |
|
= |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
1 |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
- |
- |
2 |
- |
- |
- |
- |
- |
|
|
|
occurs |
x |
|
= |
|
= |
|
- |
-- |
- |
- |
- |
- |
|
- |
- |
|
|
occurs |
x |
|
= |
|
= |
|
4 |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
-` |
- |
- |
- |
- |
- |
- |
|
|
|
|
occurs |
x |
|
= |
|
= |
|
6 |
-- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
7 |
-- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
- |
- |
- |
|
- |
- |
- |
- |
- |
- |
|
occurs |
x |
|
= |
|
= |
|
- |
- |
- |
- |
|
|
- |
- |
- |
- |
|
occurs |
x |
|
= |
|
1+8 |
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+8 |
- |
|
|
|
|
|
|
|
|
2+7 |
- |
|
- |
- |
3+6 |
- |
2+7 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
- |
|
|
|
- |
- |
|
|
- |
8 |
- |
9 |
- |
- |
|
|
|
1+7 |
= |
|
= |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
|
|
2 |
= |
9 |
= |
3 |
5 |
|
|
|
1+9 |
= |
|
1+0 |
|
|
|
|
20 |
- |
18 |
- |
3 |
5 |
|
|
|
4+6 |
= |
|
1+0 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
20 |
8 |
18 |
9 |
3 |
5 |
|
|
|
6+3 |
= |
|
= |
|
|
|
|
2 |
8 |
9 |
9 |
3 |
5 |
|
|
|
3+6 |
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
2 |
- |
- |
- |
- |
- |
|
|
|
occurs |
x |
|
= |
|
= |
|
-- |
- |
- |
- |
- |
|
- |
- |
|
|
occurs |
x |
|
= |
|
= |
|
- |
- |
- |
- |
- |
- |
|
|
|
|
occurs |
x |
|
= |
|
= |
|
- |
- |
|
- |
- |
- |
- |
- |
- |
|
occurs |
x |
|
= |
|
= |
|
- |
- |
- |
|
|
- |
- |
- |
- |
|
occurs |
x |
|
= |
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
2+7 |
- |
|
- |
- |
3+6 |
- |
2+7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
63 |
36 |
9 |
6 |
|
63 |
36 |
9 |
6 |
|
63 |
36 |
9 |
18 |
- |
|
|
|
1+8 |
- |
1+8+9 |
1+0+8 |
2+7 |
9 |
- |
|
|
|
|
- |
1+8 |
- |
- |
6 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
3 |
|
|
|
|
A |
1 |
1 |
1 |
|
|
|
|
|
12 |
3 |
3 |
|
|
|
|
|
3 |
3 |
3 |
|
|
|
|
|
21 |
3 |
3 |
|
|
|
|
|
12 |
3 |
3 |
|
|
|
|
|
21 |
3 |
3 |
|
|
|
|
S |
19 |
10 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9+2 |
2+9 |
2+9 |
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
1+1 |
1+1 |
1+1 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
19 |
|
|
|
1+9 |
|
|
1+0 |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
3 |
1 |
3 |
3 |
3 |
3 |
3 |
|
|
|
|
1+9 |
|
|
1+0 |
|
|
|
- |
- |
3 |
1 |
12 |
3 |
21 |
12 |
21 |
|
|
|
|
7+3 |
|
|
1+0 |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
3 |
1 |
12 |
3 |
21 |
12 |
21 |
19 |
|
|
|
9+2 |
|
|
1+0 |
|
|
|
- |
- |
3 |
1 |
3 |
3 |
3 |
3 |
3 |
1 |
|
|
|
2+0 |
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
occurs |
x |
|
= |
|
|
|
2 |
- |
|
|
|
|
|
|
|
- |
- |
- |
2 |
TWO |
2 |
- |
- |
- |
- |
- |
|
- |
3 |
|
3 |
3 |
3 |
3 |
3 |
- |
- |
- |
|
occurs |
x |
|
= |
|
1+8 |
|
|
- |
|
|
|
|
|
|
|
- |
- |
- |
4 |
FOUR |
4 |
- |
- |
- |
- |
- |
|
- |
|
|
|
|
|
|
|
- |
- |
- |
5 |
FIVE |
5 |
- |
- |
- |
- |
- |
6 |
- |
|
|
|
|
|
|
|
- |
- |
- |
6 |
SIX |
6 |
- |
- |
- |
- |
- |
|
- |
|
|
|
|
|
|
|
- |
- |
- |
7 |
SEVEN |
7 |
- |
- |
- |
- |
- |
8 |
- |
|
|
|
|
|
|
|
- |
- |
- |
8 |
EIGHT |
8 |
- |
- |
- |
- |
- |
9 |
|
|
|
|
|
- |
|
- |
|
|
|
9 |
NINE |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4+1 |
- |
3 |
|
3 |
3 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
2+0 |
|
2+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
3 |
3 |
3 |
3 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
19 |
|
|
|
1+9 |
|
|
1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
3 |
1 |
3 |
3 |
3 |
3 |
3 |
|
|
|
|
1+9 |
|
|
1+0 |
|
|
|
- |
3 |
1 |
12 |
3 |
21 |
12 |
21 |
|
|
|
|
7+3 |
|
|
1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
3 |
1 |
12 |
3 |
21 |
12 |
21 |
19 |
|
|
|
9+2 |
|
|
1+0 |
|
|
|
- |
3 |
1 |
3 |
3 |
3 |
3 |
3 |
1 |
|
|
|
2+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
occurs |
x |
|
= |
|
|
|
|
3 |
|
3 |
3 |
3 |
3 |
3 |
|
|
|
|
occurs |
x |
|
= |
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
3 |
|
3 |
3 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
2+0 |
|
2+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
3 |
3 |
3 |
3 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4
|
ZERO |
64 |
28 |
1 |
|
3
|
ONE |
34
|
16
|
7
|
|
3
|
TWO |
58
|
13
|
4
|
|
5
|
THREE |
56
|
29
|
2
|
|
4
|
FOUR |
60
|
24
|
6
|
|
4
|
FIVE |
42
|
24
|
6
|
|
3
|
SIX |
52
|
16
|
7
|
|
5
|
SEVEN |
65
|
20
|
2
|
|
5
|
EIGHT |
49
|
31
|
4
|
|
4
|
NINE |
42
|
24
|
6
|
40 |
- |
522 |
225 |
45 |
4+0 |
- |
5+2+2 |
2+2+5 |
4+5 |
4 |
- |
9 |
9 |
9 |
O |
= |
6 |
3 |
|
34 |
16 |
7 |
T |
= |
2 |
3 |
|
58 |
13 |
4 |
T |
= |
2 |
5 |
|
56 |
29 |
2 |
F |
= |
6 |
4 |
|
60 |
24 |
6 |
F |
= |
6 |
4 |
|
42 |
24 |
6 |
S |
= |
1 |
3 |
|
52 |
16 |
7 |
S |
= |
1 |
5 |
|
65 |
20 |
2 |
E |
= |
5 |
5 |
|
49 |
31 |
4 |
N |
= |
5 |
4 |
|
42 |
24 |
6 |
- |
- |
39 |
36 |
- |
|
|
|
- |
- |
3+9 |
3+6 |
- |
4+5+8 |
1+9+7 |
4+4 |
- |
- |
12 |
9 |
- |
|
|
|
- |
- |
1+2 |
|
- |
1+7 |
1+7 |
- |
- |
- |
3 |
9 |
- |
|
|
|
Z |
= |
8 |
4 |
|
64 |
28 |
1 |
O |
= |
6 |
3 |
|
34 |
16 |
7 |
S |
= |
1 |
5 |
|
65 |
20 |
2 |
T |
= |
2 |
3 |
|
58 |
13 |
4 |
F |
= |
6 |
4 |
|
60 |
24 |
6 |
S |
= |
1 |
3 |
|
52 |
16 |
7 |
T |
= |
2 |
5 |
|
56 |
29 |
2 |
F |
= |
6 |
4 |
|
42 |
24 |
6 |
E |
= |
5 |
5 |
|
49 |
31 |
4 |
N |
= |
5 |
4 |
|
42 |
24 |
6 |
- |
- |
47 |
40 |
- |
|
|
|
- |
- |
11 |
4+0 |
- |
5+2+2 |
2+2+5 |
4+5 |
- |
- |
2 |
4 |
- |
|
|
|
1 |
3 |
|
O |
= |
15 |
= |
6 |
2 |
3 |
|
T |
= |
20 |
= |
2 |
3 |
5 |
|
T |
= |
20 |
= |
2 |
4 |
4 |
|
F |
= |
6 |
= |
6 |
5 |
4 |
|
F |
= |
6 |
= |
6 |
6 |
3 |
|
S |
= |
19 |
= |
1 |
7 |
5 |
|
S |
= |
19 |
= |
1 |
8 |
5 |
|
E |
= |
5 |
= |
5 |
9 |
4 |
|
N |
= |
14 |
= |
5 |
45 |
36 |
- |
- |
- |
124 |
- |
34 |
4+5 |
3+6 |
- |
- |
- |
1+2+4 |
- |
3+4 |
9 |
9 |
- |
- |
- |
7 |
- |
7 |
|
|
- |
- |
- |
1+2 |
- |
1+2 |
9 |
9 |
- |
- |
- |
3 |
- |
3 |
|
15 |
O |
|
|
- |
|
|
O |
- |
|
H |
|
|
|
- |
F |
O |
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
6 |
5 |
|
- |
|
|
6 |
- |
|
8 |
|
|
|
- |
|
6 |
|
|
|
|
|
3+1 |
|
|
|
|
|
|
- |
- |
15 |
14 |
|
- |
|
|
15 |
- |
|
8 |
|
|
|
- |
|
15 |
|
|
|
|
|
6+7 |
|
|
1+3 |
|
|
|
|
15 |
O |
|
|
- |
|
|
O |
- |
|
H |
|
|
|
- |
F |
O |
|
|
|
|
|
|
|
|
|
- |
|
|
- |
- |
|
|
5 |
- |
2 |
5 |
|
- |
2 |
|
9 |
5 |
5 |
- |
6 |
|
3 |
9 |
|
|
|
5+1 |
|
|
|
|
|
|
- |
- |
|
|
5 |
- |
20 |
23 |
|
- |
20 |
|
18 |
5 |
5 |
- |
6 |
|
21 |
18 |
|
|
|
1+4+1 |
|
|
|
|
|
|
|
15 |
O |
|
|
- |
|
|
O |
- |
|
H |
|
|
|
- |
F |
O |
|
|
|
|
|
|
|
|
|
- |
|
|
- |
- |
15 |
14 |
5 |
- |
20 |
23 |
15 |
- |
20 |
8 |
18 |
5 |
5 |
- |
6 |
15 |
21 |
18 |
|
|
|
2+0+8 |
|
|
1+0 |
|
|
|
- |
- |
6 |
5 |
5 |
- |
2 |
5 |
6 |
- |
2 |
8 |
9 |
5 |
5 |
- |
6 |
6 |
3 |
9 |
|
|
|
8+2 |
|
|
1+0 |
|
|
|
|
15 |
O |
|
|
- |
|
|
O |
- |
|
H |
|
|
|
- |
F |
O |
|
|
|
|
|
|
|
|
|
- |
- |
|
|
- |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
|
|
- |
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
3 |
|
|
|
- |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
2+5 |
|
- |
- |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
24 |
2+4 |
|
|
- |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-`` |
- |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
8 |
|
|
|
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
1+8 |
|
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+2 |
1+5 |
|
|
|
- |
- |
|
|
- |
- |
|
|
|
|
- |
|
|
|
|
|
|
3+3 |
|
|
1+5 |
|
8+2 |
|
3+7 |
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
- |
- |
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
1+0 |
|
1+0 |
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
O |
|
|
- |
|
|
O |
- |
|
H |
|
|
|
- |
F |
O |
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
6 |
5 |
|
- |
|
|
6 |
- |
|
8 |
|
|
|
- |
|
6 |
|
|
|
|
|
3+1 |
|
|
= |
|
|
|
- |
15 |
14 |
|
- |
|
|
15 |
- |
|
8 |
|
|
|
- |
|
15 |
|
|
|
|
|
6+7 |
|
|
1+3 |
|
|
|
15 |
O |
|
|
- |
|
|
O |
- |
|
H |
|
|
|
- |
F |
O |
|
|
|
|
|
|
|
|
|
- |
|
|
- |
|
|
5 |
- |
2 |
5 |
|
- |
2 |
|
9 |
5 |
5 |
- |
6 |
|
3 |
9 |
|
|
|
5+1 |
|
|
= |
|
|
|
- |
|
|
5 |
- |
20 |
23 |
|
- |
20 |
|
18 |
5 |
5 |
- |
6 |
|
21 |
18 |
|
|
|
1+4+1 |
|
|
= |
|
|
|
15 |
O |
|
|
- |
|
|
O |
- |
|
H |
|
|
|
- |
F |
O |
|
|
|
|
|
|
|
|
|
- |
|
|
- |
15 |
14 |
5 |
- |
20 |
23 |
15 |
- |
20 |
8 |
18 |
5 |
5 |
- |
6 |
15 |
21 |
18 |
|
|
|
2+0+8 |
|
|
1+0 |
|
|
|
- |
6 |
5 |
5 |
- |
2 |
5 |
6 |
- |
2 |
8 |
9 |
5 |
5 |
- |
6 |
6 |
3 |
9 |
|
|
|
8+2 |
|
|
1+0 |
|
|
|
15 |
O |
|
|
- |
|
|
O |
- |
|
H |
|
|
|
- |
F |
O |
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
= |
|
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
3 |
= |
|
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
2+5 |
|
- |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
24 |
2+4 |
|
- |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
8 |
= |
|
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
1+8 |
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+5 |
|
|
|
- |
- |
|
|
- |
- |
|
|
|
|
- |
|
|
|
|
|
|
3+3 |
|
|
1+5 |
|
8+2 |
|
3+7 |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
- |
- |
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
1+0 |
|
1+0 |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
- |
|
I |
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
5 |
9 |
5 |
|
- |
|
9 |
|
8 |
|
- |
1 |
|
|
|
5 |
- |
1 |
9 |
6 |
|
|
|
5+8 |
|
|
1+3 |
|
|
|
- |
- |
14 |
9 |
14 |
|
- |
|
9 |
|
8 |
|
- |
19 |
|
|
|
14 |
- |
19 |
9 |
24 |
|
|
|
1+3+9 |
|
|
1+3 |
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
- |
|
I |
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
|
|
|
5 |
- |
5 |
|
7 |
|
2 |
- |
|
5 |
4 |
5 |
|
- |
|
|
|
|
|
|
3+3 |
|
|
= |
|
|
|
- |
- |
|
|
|
5 |
- |
5 |
|
7 |
|
20 |
- |
|
5 |
22 |
5 |
|
- |
|
|
|
|
|
|
6+9 |
|
|
1+5 |
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
- |
|
I |
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
14 |
9 |
14 |
5 |
- |
5 |
9 |
7 |
8 |
20 |
- |
19 |
5 |
22 |
5 |
14 |
- |
19 |
9 |
24 |
|
|
|
2+0+8 |
|
|
1+0 |
|
|
|
- |
- |
5 |
9 |
5 |
5 |
- |
5 |
9 |
7 |
8 |
2 |
- |
1 |
5 |
4 |
5 |
5 |
- |
1 |
9 |
6 |
|
|
|
9+1 |
|
|
1+0 |
|
|
|
|
17 |
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
= |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
2 |
= |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
4 |
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
4 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
occurs |
x |
|
= |
35 |
3+5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
6 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
7 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
8 |
= |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
occurs |
x |
|
= |
27 |
2+7 |
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
1+7 |
- |
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
4+2 |
|
|
1+7 |
|
9+1 |
|
4+6 |
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
1+0 |
|
1+0 |
|
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
ONE TWO THREE FOUR |
208 |
82 |
1 |
17 |
NINE EIGHT SEVEN SIX |
208 |
91 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
6 |
|
4 |
5 |
|
|
|
1+5 |
|
|
|
|
- |
- |
6 |
|
22 |
5 |
|
|
|
3+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
6 |
9 |
22 |
5 |
|
|
|
4+2 |
|
|
|
|
- |
- |
6 |
9 |
4 |
5 |
|
|
|
2+4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
- |
|
4 |
- |
|
|
|
occurs |
x |
|
= |
4 |
|
|
- |
|
- |
5 |
|
|
|
occurs |
x |
|
= |
5 |
|
|
|
- |
- |
- |
|
|
|
occurs |
x |
|
= |
|
|
|
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
- |
9 |
|
|
|
|
|
occurs |
x |
|
= |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+1 |
|
|
|
|
|
|
|
2+4 |
|
|
|
|
2+4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
6 |
|
4 |
5 |
|
|
|
1+5 |
|
|
|
|
- |
6 |
|
22 |
5 |
|
|
|
3+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
6 |
9 |
22 |
5 |
|
|
|
4+2 |
|
|
|
|
- |
6 |
9 |
4 |
5 |
|
|
|
2+4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
|
4 |
- |
|
|
|
occurs |
x |
|
= |
4 |
|
- |
|
- |
5 |
|
|
|
occurs |
x |
|
= |
5 |
|
|
- |
- |
- |
|
|
|
occurs |
x |
|
= |
|
|
- |
9 |
|
|
|
|
|
occurs |
x |
|
= |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+4 |
|
|
|
|
2+4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
ONE TWO THREE FOUR |
208 |
82 |
1 |
4 |
FIVE |
42 |
24 |
6 |
17 |
NINE EIGHT SEVEN SIX |
208 |
91 |
1 |
|
3
|
ONE |
34
|
16
|
7
|
|
3
|
TWO |
58
|
13
|
4
|
|
5
|
THREE |
56
|
29
|
2
|
|
4
|
FOUR |
60
|
24
|
6
|
15 |
|
208 |
82 |
1 |
| |
|
|
|
|
| |
|
|
|
|
|
4
|
FIVE |
42
|
24
|
6
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
3
|
SIX |
52
|
16
|
7
|
|
5
|
SEVEN |
65
|
20
|
2
|
|
5
|
EIGHT |
49
|
31
|
4
|
|
4
|
NINE |
42
|
24
|
6
|
17 |
- |
208 |
91 |
1 |
|
3
|
ONE |
34
|
16
|
7
|
|
3
|
TWO |
58
|
13
|
4
|
|
5
|
THREE |
56
|
29
|
2
|
|
4
|
FOUR |
60
|
24
|
6
|
15 |
|
208 |
82 |
1 |
| |
|
|
|
|
| |
|
|
|
|
|
4
|
FIVE |
42
|
24
|
6
|
| |
|
|
|
|
| |
|
|
|
|
17 |
- |
208 |
91 |
1 |
|
4
|
NINE |
42
|
24
|
6
|
|
5
|
EIGHT |
49
|
31
|
4
|
|
5
|
SEVEN |
65
|
20
|
2
|
|
3
|
SIX |
52
|
16
|
7
|
|
4
|
ZERO |
64
|
28
|
1
|
|
3
|
ONE |
34
|
16
|
7
|
|
3
|
TWO |
58
|
13
|
4
|
|
5
|
THREE |
56
|
29
|
2
|
|
4
|
FOUR |
60
|
24
|
6
|
|
4
|
FIVE |
42
|
24
|
6
|
|
3
|
SIX |
52
|
16
|
7
|
|
5
|
SEVEN |
65
|
20
|
2
|
|
5
|
EIGHT |
49
|
31
|
4
|
|
4
|
NINE |
42
|
24
|
6
|
40 |
- |
522 |
225 |
45 |
4+0 |
- |
5+2+2 |
2+2+5 |
4+5 |
4 |
- |
9 |
9 |
9 |
O |
= |
6 |
3 |
|
34 |
16 |
7 |
T |
= |
2 |
5 |
|
56 |
29 |
2 |
F |
= |
6 |
4 |
|
42 |
24 |
6 |
S |
= |
1 |
5 |
|
65 |
20 |
2 |
N |
= |
5 |
4 |
|
42 |
24 |
6 |
- |
- |
20 |
21 |
- |
|
|
|
- |
- |
2+0 |
2+1 |
- |
2+3+9 |
1+1+3 |
2+3 |
- |
- |
2 |
3 |
- |
|
|
|
- |
- |
- |
|
- |
1+3 |
- |
- |
- |
- |
2 |
3 |
- |
|
|
|
T |
= |
2 |
3 |
|
58 |
13 |
4 |
F |
= |
6 |
4 |
|
60 |
24 |
6 |
S |
= |
1 |
3 |
|
52 |
16 |
7 |
E |
= |
5 |
5 |
|
49 |
31 |
4 |
- |
- |
14 |
15 |
- |
|
|
|
- |
- |
1+4 |
1+5 |
- |
2+1+9 |
8+4 |
2+1 |
- |
- |
5 |
6 |
- |
|
|
|
- |
- |
- |
|
- |
1+2 |
1+2 |
- |
- |
- |
5 |
6 |
- |
|
|
|
Z |
= |
8 |
4 |
|
64 |
28 |
1 |
O |
= |
6 |
3 |
|
34 |
16 |
7 |
S |
= |
1 |
5 |
|
65 |
20 |
2 |
T |
= |
2 |
3 |
|
58 |
13 |
4 |
F |
= |
6 |
4 |
|
60 |
24 |
6 |
S |
= |
1 |
3 |
|
52 |
16 |
7 |
- |
- |
24 |
22 |
- |
|
|
|
- |
- |
2+4 |
2+2 |
- |
3+3+3 |
1+1+7 |
2+7 |
`- |
- |
6 |
4 |
- |
|
|
|
T |
= |
2 |
5 |
|
56 |
29 |
2 |
F |
= |
6 |
4 |
|
42 |
24 |
6 |
E |
= |
5 |
5 |
|
49 |
31 |
4 |
N |
= |
5 |
4 |
|
42 |
24 |
6 |
- |
- |
23 |
18 |
- |
|
|
|
- |
- |
2+3 |
1+8 |
- |
1+8+9 |
1+0+8 |
1+8 |
=- |
- |
5 |
9 |
- |
|
|
|
- |
- |
- |
|
- |
1+8 |
- |
- |
- |
- |
5 |
9 |
- |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
19 |
|
|
|
1+9 |
|
|
1+0 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
3 |
1 |
12 |
3 |
21 |
12 |
3 |
19 |
|
|
|
9+2 |
|
|
1+1 |
|
|
|
- |
3 |
1 |
3 |
3 |
3 |
3 |
3 |
1 |
|
|
|
2+0 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
2 |
= |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+0 |
|
1+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CURRICULUM |
|
|
|
|
C |
3 |
3 |
|
|
U |
21 |
3 |
|
|
R |
18 |
9 |
|
|
R |
18 |
9 |
|
|
I |
9 |
9 |
|
|
C |
3 |
3 |
|
|
U |
21 |
3 |
|
|
L |
12 |
3 |
|
|
U |
21 |
3 |
|
|
M |
13 |
4 |
|
10 |
CURRICULUM |
139 |
49 |
49 |
1+0 |
- |
1+3+9 |
4+9 |
4+9 |
1 |
CURRICULUM |
13 |
13 |
13 |
- |
- |
1+3 |
1+3 |
1+3 |
1 |
CURRICULUM |
4 |
4 |
4 |
|
|
|
|
|
R |
|
|
U |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
U |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
3 |
3 |
9 |
9 |
|
3 |
3 |
3 |
3 |
4 |
|
|
|
4+0 |
|
|
|
|
|
|
- |
- |
3 |
21 |
18 |
18 |
|
3 |
21 |
12 |
21 |
13 |
|
|
|
1+3+0 |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
U |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
3 |
21 |
18 |
18 |
9 |
3 |
21 |
12 |
21 |
13 |
|
|
|
1+3+9 |
|
|
|
|
|
|
- |
- |
3 |
3 |
9 |
9 |
9 |
3 |
3 |
3 |
3 |
4 |
|
|
|
4+9 |
|
|
1+3 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
18 |
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
= |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
2+7 |
|
29 |
10 |
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+9 |
1+0 |
|
|
|
9 |
9 |
|
- |
|
|
|
|
|
1+6 |
|
|
1+0 |
|
4+9 |
|
2+2 |
11 |
1 |
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+1 |
|
|
|
|
- |
- |
|
- |
|
|
|
|
|
- |
|
|
- |
|
1+3 |
|
- |
2 |
1 |
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
U |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
U |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
3 |
3 |
9 |
9 |
|
3 |
3 |
3 |
3 |
4 |
|
|
|
4+0 |
|
|
|
|
|
|
- |
- |
3 |
21 |
18 |
18 |
|
3 |
21 |
12 |
21 |
13 |
|
|
|
1+3+0 |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
U |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
3 |
21 |
18 |
18 |
9 |
3 |
21 |
12 |
21 |
13 |
|
|
|
1+3+9 |
|
|
|
|
|
|
- |
- |
3 |
3 |
9 |
9 |
9 |
3 |
3 |
3 |
3 |
4 |
|
|
|
4+9 |
|
|
1+3 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
18 |
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
2+7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+9 |
1+0 |
|
|
|
|
9 |
|
|
|
|
|
|
|
1+6 |
|
|
1+0 |
|
4+9 |
|
2+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+1 |
|
|
9 |
9 |
9 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
1+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
8 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
| - |
- |
- |
- |
- |
- |
- |
- |
9 |
9 |
|
|
|
1+8 |
|
|
|
|
|
|
11 |
8 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
3 |
1 |
3 |
3 |
3 |
3 |
|
|
|
|
|
1+6 |
|
|
|
|
|
|
- |
- |
3 |
1 |
12 |
3 |
21 |
12 |
|
|
|
|
|
5+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
- |
- |
3 |
1 |
12 |
3 |
21 |
12 |
9 |
9 |
|
|
|
7+0 |
|
|
|
|
|
|
- |
- |
3 |
1 |
3 |
3 |
3 |
3 |
9 |
9 |
|
|
|
3+4 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
1 |
|
|
2 |
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
2 |
- |
- |
- |
- |
- |
- |
- |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
1+5 |
|
4 |
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
4 |
- |
- |
- |
- |
- |
- |
- |
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5 |
- |
- |
- |
- |
- |
- |
- |
6 |
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
6 |
- |
- |
- |
- |
- |
- |
- |
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
7 |
- |
- |
- |
- |
- |
- |
- |
8 |
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
18 |
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3+2 |
|
- |
|
|
|
|
|
|
|
|
|
1+3 |
|
|
|
|
3+4 |
|
1+6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
3 |
3 |
3 |
3 |
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
|
|
|
|
|
|
|
|
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
- |
3 |
1 |
3 |
3 |
3 |
3 |
|
|
|
|
|
1+6 |
|
|
|
|
|
|
- |
3 |
1 |
12 |
3 |
21 |
12 |
|
|
|
|
|
5+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
- |
3 |
1 |
12 |
3 |
21 |
12 |
9 |
9 |
|
|
|
7+0 |
|
|
|
|
|
|
- |
3 |
1 |
3 |
3 |
3 |
3 |
9 |
9 |
|
|
|
3+4 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
- |
- |
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
1+5 |
|
- |
- |
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
18 |
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
1+3 |
|
|
|
|
3+4 |
|
1+6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
3 |
3 |
3 |
3 |
9 |
9 |
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Children of Llullaillaco, sacrificed by the Incas 500 years ago. It is believed the Children of Llullaillaco, as they have come to be known, were sacrificed during a ceremony thanking the Inca gods for the annual corn ... www.democraticunderground.com/discuss/duboard. http://news.bbc.co.uk/1/hi/world/americas/6983300.stm
Mummified Inca maiden wows crowds
"A mummy of an Inca girl, described as "perfect" by the archaeologists who found her in 1999, has gone on display for the first time in Argentina .
Hundreds of people crowded into a museum in the north-western city of Salta to see "la Doncella", the Maiden. The remains of the girl, who was 15 when she died, were found in an icy pit on top of a volcano in the Andes, along with a younger boy and girl. Researchers believe they were sacrificed by the Incas 500 years ago.
The three were discovered at a height of 6,700m (22,000ft) on Mount Llullaillaco, a volcano in north-west Argentina on the border with Chile. At the time, the archaeologist leading the team, Dr Johan Reinhard, said they appeared "the best preserved of any mummy I've seen". It is believed the Children of Llullaillaco, as they have come to be known, were sacrificed during a ceremony thanking the Inca gods for the annual corn harvest.
'Great mistake' The mummy of la Doncella is on display in a chamber that is filled with cold air that recreates the sub-freezing conditions in which she was found. Visitors told Argentina media they were impressed at the mummy's state of conservation. "I'm amazed," one woman said. "You just expect her at any moment to get up and start talking." But the exhibition has angered several indigenous groups who campaigned to stop the mummy from going on display.
Miguel Suarez from the Calchaquies valley tribes in and around Salta told the Associated Press news agency that the exhibit was "a great mistake", adding that he hoped visitors would show respect for the dead."
| - |
LLULLAILLACO |
- |
- |
- |
| 3 |
L+L+U |
45 |
9 |
9 |
| 2 |
L+L+A |
25 |
7 |
7 |
| 1 |
I |
9 |
9 |
9 |
| 3 |
L+L+A |
25 |
7 |
7 |
| 2 |
C+O |
18 |
9 |
9 |
| 12 |
LLULLAILLACO |
122 |
41 |
41 |
1+2 |
- |
1+2+2 |
4+1 |
4+1 |
| 3 |
LLULLAILLACO |
5 |
5 |
5 |
- |
- |
- |
- |
- |
| 3 |
LLULLAILLACO |
5 |
5 |
5 |
| - |
- |
- |
- |
- |
|
- |
LLULLAILLACO |
- |
- |
- |
| L |
3 |
- |
- |
- |
L |
1 |
L |
12 |
3 |
3 |
| L |
3 |
- |
- |
- |
L |
1 |
L |
12 |
3 |
3 |
| U |
3 |
- |
- |
- |
U |
1 |
U |
21 |
3 |
3 |
| L |
3 |
- |
- |
- |
L |
1 |
L |
12 |
3 |
3 |
| L |
3 |
- |
- |
- |
L |
1 |
L |
12 |
3 |
3 |
| - |
- |
A |
- |
- |
A |
1 |
A |
1 |
1 |
1 |
| - |
- |
- |
I |
- |
I |
1 |
I |
9 |
9 |
9 |
| L |
3 |
- |
- |
- |
L |
1 |
L |
12 |
3 |
3 |
| L |
3 |
- |
- |
- |
L |
1 |
L |
12 |
3 |
3 |
| - |
- |
A |
- |
- |
A |
1 |
A |
1 |
1 |
1 |
| C |
3 |
- |
- |
- |
C |
1 |
C |
3 |
3 |
3 |
| - |
- |
- |
- |
O |
O |
1 |
O |
15 |
6 |
6 |
| |
24 |
- |
- |
|
|
12 |
LLULLAILLACO |
122 |
41 |
41 |
| |
2+4 |
- |
- |
|
|
1+2 |
- |
1+2+2 |
4+1 |
4+1 |
| |
6 |
- |
- |
|
|
3 |
LLULLAILLACO |
5 |
5 |
5 |
| |
- |
- |
- |
|
|
- |
- |
- |
- |
- |
| |
1 |
- |
- |
|
|
3 |
LLULLAILLACO |
5 |
5 |
5 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
|
|
|
|
|
|
9 |
|
|
|
|
6 |
|
|
|
1+5 |
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
9 |
|
|
|
|
15 |
|
|
|
2+4 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
- |
3 |
3 |
3 |
3 |
3 |
1 |
|
3 |
3 |
1 |
3 |
|
|
|
|
2+6 |
|
|
|
|
|
|
- |
- |
12 |
12 |
21 |
12 |
12 |
1 |
|
12 |
12 |
1 |
3 |
|
|
|
|
9+8 |
|
|
1+7 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
- |
- |
12 |
12 |
21 |
12 |
12 |
1 |
9 |
12 |
12 |
1 |
3 |
15 |
|
|
|
1+2+2 |
|
|
|
|
|
|
- |
- |
3 |
3 |
3 |
3 |
3 |
1 |
9 |
3 |
3 |
1 |
3 |
6 |
|
|
|
4+1 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
2 |
|
|
2 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
24 |
2+4 |
|
4 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
6 |
|
|
7 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+6 |
1+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+9 |
|
|
1+2 |
|
4+1 |
|
2+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
3 |
3 |
3 |
1 |
|
3 |
3 |
1 |
3 |
6 |
|
|
1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
|
|
|
|
|
|
9 |
|
|
|
|
6 |
|
|
|
1+5 |
|
|
|
|
|
|
- |
|
|
|
|
|
|
9 |
|
|
|
|
15 |
|
|
|
2+4 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
3 |
3 |
3 |
3 |
3 |
1 |
|
3 |
3 |
1 |
3 |
|
|
|
|
2+6 |
|
|
|
|
|
|
- |
12 |
12 |
21 |
12 |
12 |
1 |
|
12 |
12 |
1 |
3 |
|
|
|
|
9+8 |
|
|
1+7 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
- |
12 |
12 |
21 |
12 |
12 |
1 |
9 |
12 |
12 |
1 |
3 |
15 |
|
|
|
1+2+2 |
|
|
|
|
|
|
- |
3 |
3 |
3 |
3 |
3 |
1 |
9 |
3 |
3 |
1 |
3 |
6 |
|
|
|
4+1 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
24 |
2+4 |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
6 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+9 |
|
|
1+2 |
|
4+1 |
|
2+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
3 |
3 |
3 |
1 |
|
3 |
3 |
1 |
3 |
6 |
|
|
1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The civilisation we discuss, which does not appear to have found a need to develop writing, is that of the Incas. The Inca empire which existed in 1532, ... www-history.mcs.st-andrews.ac.uk/HistTopics/Inca_mathematics
History topic: Mathematics of the Incas
It is often thought that mathematics can only develop after a civilisation has developed some form of writing. Although not easy for us to understand today, many civilisations reached highly advanced states without ever developing written records. Now of course it is difficult for us to know much about such civilisations since there is no written record to be studied today. This article looks at the mathematical achievements of one such civilisation.
The civilisation we discuss, which does not appear to have found a need to develop writing, is that of the Incas. The Inca empire which existed in 1532, before the Spanish conquest, was vast. It spread over an area which stretched from what is now the northern border of Ecuador to Mendoza in west-central Argentina and to the Maule River in central Chile. The Inca people numbered around 12 million but they were from many different ethnic groups and spoke about 20 different languages. The civilisation had reached a high level of sophistication with a remarkable system of roads, agriculture, textile design, and administration. Of course even if writing is not required to achieve this level, counting and recording of numerical information is necessary. The Incas had developed a method of recording numerical information which did not require writing. It involved knots in strings called quipu.
The quipu was not a calculator, rather it was a storage device. Remember that the Incas had no written records and so the quipu played a major role in the administration of the Inca empire since it allowed numerical information to be kept. Let us first describe the basic quipu, with its positional number system, and then look at the ways that it was used in Inca society.
The quipu consists of strings which were knotted to represent numbers. A number was represented by knots in the string, using a positional base 10 representation. If the number 586 was to be recorded on the string then six touching knots were placed near the free end of the string, a space was left, then eight touching knots for the 10s, another space, and finally 5 touching knots for the 100s.
(Illustration omitted) 586 on a quipu.
For larger numbers more knot groups were used, one for each power of 10, in the same way as the digits of the number system we use here are occur in different positions to indicate the number of the corresponding power of 10 in that position.
Now it is not quite true that the same knots were used irrespective of the position as would be the case in a true positional system. There seems only one exception, namely the unit position, where different styles of knots were used from those in the other positions. In fact two different styles were used in the units position, one style if the unit were a 1 and a second style if the unit were greater than one. Both these styles differed from the standard knot used for all other positions. The system had a zero position, for this would be represented as no knots in that position. This meant that the spacing had to be highly regular so that zero positions would be clear.
There are many drawings and descriptions of quipus made by the Spanish invaders. Garcilaso de la Vega, whose mother was an Inca and whose father was Spanish, wrote (see for example [5]):-
According to their position, the knots signified units, tens, hundreds, thousands, ten thousands and, exceptionally, hundred thousands, and they are all well aligned on their different cords as the figures that an accountant sets down, column by column, in his ledger.
Now of course recording a number on a string would, in itself, not be that useful. A quipu had many strings and there had to be some way that the string carrying the record of a particular number could be identified. The primary way this was done was by the use of colour. Numbers were recorded on strings of a particular colour to identify what that number was recording. For example numbers of cattle might be recorded on green strings while numbers of sheep might be recorded on white strings. The colours each had several meanings, some of which were abstract ideas, some concrete as in the cattle and sheep example. White strings had the abstract meaning of "peace" while red strings had the abstract meaning of "war"
As well as the colour coding, another way of distinguishing the strings was to make some strings subsidiary ones, tied to the middle of a main string rather than being tied to the main horizontal cord.
(Illustration omitted) Quipu with subsidiary cords.
We quote Garcilaso de la Vega again [5]:-
The ordinary judges gave a monthly account of the sentences they imposed to their superiors, and they in turn reported to their immediate superiors, and so on finally to the Inca or those of his Supreme Council. The method of making these reports was by means of knots, made of various colours, where knots of such and such colours denote that such and such crimes had been punished. Smaller threads attached to thicker cords were of different colours to signify the precise nature of the punishment that had been inflicted.
It was not only judges who sent quipus to be kept in a central record. The Inca king appointed quipucamayocs, or keepers of the knots, to each town. Larger towns might have had up to thirty quipucamayocs who were essentially government statisticians, keeping official census records of the population, records of the produce of the town, its animals and weapons. This and other information was sent annually to the capital Cuzco. There was even an official delivery service to take to quipus to Cuzco which consisted of relay runners who passed the quipus on to the next runner at specially constructed staging posts. The terrain was extremely difficult yet the Incas had constructed roads to make the passing of information by quipus surprisingly rapid.
Much information on the quipus comes from a letter of the Peruvian Felipe Guaman Poma de Ayala to the King of Spain, written about eighty years after the Spanish conquest of the Incas. This remarkable letter contains 1179 pages and there are several drawings which show quipus. A fascinating aspect of one of these drawing is a picture of a counting board in the bottom left hand corner of one of them. This is called the yupana and is presumed to be the counting board of the Incas.
(Illustration omitted) This is what the yupana looked like.
Interpretations of how this counting board, or Peruvian abacus, might have been used have been given by several authors, see for example [9] and [11]. However some historians are less certain that this really is a Peruvian abacus. For example [2] in which the authors write:-
It is unclear from Poma's commentary whether it is his version of a device associated with Spanish activities analogous to those of the person depicted or whether he is implying its association with the Incas. In either case, his commentary makes interpretation of the configuration and the meaning of the unfilled and filled holes highly speculative.
It is a difficult task to gain further insights into the mathematical understanding of the Incas. The book [6] by Urton is interesting for it examines the concept of number as understood by the Inca people. As one might expect, their concept of number was a very concrete one, unlike our concept of number which is a highly abstract one (although this is not really understood by many people). The concrete way of conceiving numbers is illustrated by different words used when describing properties of numbers. One example given in [6] is that of even and odd numbers. Now the ideas of an even number, say, relies on having an abstract concept of number which is independent of the objects being counted. However, the Peruvian languages had different words which applied to different types of objects. For example separate words occur for the idea of [6]:-
... the two together that make a pair ...
... the one together with its mate ...
... two - in reference to one thing that is divided into two parts ...
... a pair of two separate things bound intimately together, such as two bulls yoked together for ploughing ... etc.
This is a fascinating topic and one which deserves much further research. One wonders whether the Incas applied their number system to solve mathematical problems. Was it merely for recording? If the yupana really was an abacus then it must have been used to solve problems and this prompts the intriguing question of what these problems were. A tantalising glimpse may be contained in the writings of the Spanish priest José de Acosta who lived among the Incas from 1571 to 1586. He writes in his book Historia Natural Moral de las Indias which was published in Madrid in 1596:-
To see them use another kind of calculator, with maize kernels, is a perfect joy. In order to carry out a very difficult computation for which an able computer would require pen and paper, these Indians make use of their kernels. They place one here, three somewhere else and eight, I know not where. They move one kernel here and there and the fact is that they are able to complete their computation without making the smallest mistake. as a matter of fact, they are better at practical arithmetic than we are with pen and ink. Whether this is not ingenious and whether these people are wild animals let those judge who will! What I consider ascertain is that in what they undertake to do they are superior to us.
What a pity that de Acosta did not have the mathematical skills to give a precise description which would have allowed us to understand this method of calculation by the Incas.
Article by: J J O'Connor and E F Robertson January 2001 MacTutor History of Mathematics
[http://www-history.mcs.st-andrews.ac.uk/HistTopics/Inca_mathematics.html]
- |
MATHEMATICS |
- |
- |
- |
4 |
|
42 |
15 |
|
2 |
|
18 |
9 |
|
2 |
|
21 |
3 |
|
1 |
|
9 |
9 |
|
2 |
|
22 |
4 |
|
|
MATHEMATICS |
|
|
|
|
|
1+1+2 |
4+0 |
3+1 |
|
MATHEMATICS |
|
|
|
THE MAGIC MOUNTAIN
Thomas Mann
1875-1955
Page 417
"I preach mathematics."
SUPER SCIENCE
Michael White
1
999
"The discovery of the theory of universal gravitation took
NEWTON
almost twenty years and did not really take shape until he wrote his great book
THE
PRINCIPIA MATHEMATICA
between 1684 and its publication in 1687."
9 |
PRINCIPIA |
95 |
59 |
5 |
11 |
MATHEMATICA |
94 |
40 |
4 |
20 |
First Total |
189 |
99 |
9 |
2+0 |
Add to Reduce |
1+8+9 |
9+9 |
- |
2 |
Second Total |
18 |
18 |
9 |
- |
Reduce to Deduce |
1+8 |
1+8 |
- |
2 |
Essence of Number |
9 |
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
7 |
- |
9 |
PRINCIPIA |
95 |
59 |
5 |
- |
|
- |
|
|
|
|
|
|
|
M |
= |
4 |
- |
11 |
MATHEMATICA |
94 |
40 |
4 |
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
7 |
1 |
1 |
P |
16 |
7 |
7 |
- |
|
|
|
|
|
6 |
|
|
|
R |
= |
9 |
2 |
1 |
R |
18 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
I |
= |
9 |
3 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
N |
= |
5 |
4 |
1 |
N |
14 |
5 |
5 |
- |
|
|
|
|
|
6 |
|
|
|
C |
= |
3 |
5 |
1 |
C |
3 |
3 |
3 |
- |
|
|
|
|
|
6 |
|
|
|
I |
= |
9 |
6 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
P |
= |
7 |
7 |
1 |
P |
16 |
7 |
7 |
- |
|
|
|
|
|
6 |
|
|
|
I |
= |
9 |
8 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
A |
= |
1 |
9 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
6 |
|
|
|
M |
= |
4 |
10 |
1 |
M |
13 |
4 |
4 |
- |
|
|
- |
|
|
6 |
|
|
|
A |
= |
1 |
11 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
6 |
|
|
|
T |
= |
2 |
12 |
1 |
T |
20 |
2 |
2 |
- |
|
|
|
|
|
6 |
|
|
|
H |
= |
8 |
13 |
1 |
H |
8 |
8 |
8 |
- |
|
|
|
|
|
6 |
|
|
|
E |
= |
5 |
14 |
1 |
E |
5 |
5 |
5 |
- |
|
|
|
|
|
6 |
|
|
|
M |
= |
4 |
15 |
1 |
M |
13 |
4 |
4 |
- |
|
|
- |
|
|
6 |
|
|
|
A |
= |
1 |
16 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
6 |
|
|
|
T |
= |
2 |
17 |
1 |
T |
20 |
2 |
2 |
- |
|
|
|
|
|
6 |
|
|
|
I |
= |
9 |
18 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
C |
= |
3 |
19 |
1 |
C |
3 |
3 |
3 |
- |
|
|
|
|
|
6 |
|
|
|
A |
= |
1 |
20 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
6 |
|
|
|
|
|
99 |
|
20 |
|
189 |
99 |
99 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
99 |
|
9 |
PRINCIPIA |
95 |
59 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
9+9 |
- |
11 |
MATHEMATICA |
94 |
40 |
4 |
|
|
|
|
|
1+0 |
|
1+4 |
|
4+5 |
Q |
- |
18 |
- |
20 |
First Total |
189 |
99 |
9 |
|
|
|
|
|
1 |
|
5 |
|
9 |
- |
- |
1+8 |
- |
2+0 |
Add to Reduce |
1+8+9 |
9+9 |
- |
|
|
|
|
|
|
|
|
|
|
Q |
- |
9 |
- |
2 |
Second Total |
18 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
- |
Reduce to Deduce |
1+8 |
1+8 |
- |
|
|
|
|
|
|
|
|
|
|
Q |
- |
9 |
- |
2 |
Essence of Number |
9 |
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
7 |
- |
9 |
PRINCIPIA |
95 |
59 |
5 |
- |
|
- |
|
|
|
|
|
|
|
M |
= |
4 |
- |
11 |
MATHEMATICA |
94 |
40 |
4 |
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
= |
1 |
9 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
6 |
|
|
|
A |
= |
1 |
11 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
6 |
|
|
|
A |
= |
1 |
16 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
6 |
|
|
|
A |
= |
1 |
20 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
6 |
|
|
|
T |
= |
2 |
12 |
1 |
T |
20 |
2 |
2 |
- |
|
|
|
|
|
6 |
|
|
|
T |
= |
2 |
17 |
1 |
T |
20 |
2 |
2 |
- |
|
|
|
|
|
6 |
|
|
|
C |
= |
3 |
5 |
1 |
C |
3 |
3 |
3 |
- |
|
|
|
|
|
6 |
|
|
|
C |
= |
3 |
19 |
1 |
C |
3 |
3 |
3 |
- |
|
|
|
|
|
6 |
|
|
|
M |
= |
4 |
10 |
1 |
M |
13 |
4 |
4 |
- |
|
|
- |
|
|
6 |
|
|
|
M |
= |
4 |
15 |
1 |
M |
13 |
4 |
4 |
- |
|
|
- |
|
|
6 |
|
|
|
N |
= |
5 |
4 |
1 |
N |
14 |
5 |
5 |
- |
|
|
|
|
|
6 |
|
|
|
E |
= |
5 |
14 |
1 |
E |
5 |
5 |
5 |
- |
|
|
|
|
|
6 |
|
|
|
P |
= |
7 |
1 |
1 |
P |
16 |
7 |
7 |
- |
|
|
|
|
|
6 |
|
|
|
P |
= |
7 |
7 |
1 |
P |
16 |
7 |
7 |
- |
|
|
|
|
|
6 |
|
|
|
H |
= |
8 |
13 |
1 |
H |
8 |
8 |
8 |
- |
|
|
|
|
|
6 |
|
|
|
R |
= |
9 |
2 |
1 |
R |
18 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
I |
= |
9 |
3 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
I |
= |
9 |
6 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
I |
= |
9 |
8 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
I |
= |
9 |
18 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
6 |
|
|
|
|
|
99 |
|
20 |
|
189 |
99 |
99 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
99 |
|
9 |
PRINCIPIA |
95 |
59 |
5 |
|
|
|
|
|
|
|
|
|
|
- |
- |
9+9 |
- |
11 |
MATHEMATICA |
94 |
40 |
4 |
|
|
|
|
|
1+0 |
|
1+4 |
|
4+5 |
Q |
- |
18 |
- |
20 |
First Total |
189 |
99 |
9 |
|
|
|
|
|
1 |
|
5 |
|
9 |
- |
- |
1+8 |
- |
2+0 |
Add to Reduce |
1+8+9 |
9+9 |
- |
|
|
|
|
|
|
|
|
|
|
Q |
- |
9 |
- |
2 |
Second Total |
18 |
18 |
9 |
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
- |
Reduce to Deduce |
1+8 |
1+8 |
- |
|
|
|
|
|
|
|
|
|
|
Q |
- |
9 |
- |
2 |
Essence of Number |
9 |
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
7 |
- |
9 |
PRINCIPIA |
95 |
59 |
5 |
- |
|
- |
|
|
|
|
|
|
M |
= |
4 |
- |
11 |
MATHEMATICA |
94 |
40 |
4 |
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
= |
1 |
9 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
|
|
|
A |
= |
1 |
11 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
|
|
|
A |
= |
1 |
16 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
|
|
|
A |
= |
1 |
20 |
1 |
A |
1 |
1 |
1 |
- |
|
|
|
|
|
|
|
|
T |
= |
2 |
12 |
1 |
T |
20 |
2 |
2 |
- |
|
|
|
|
|
|
|
|
T |
= |
2 |
17 |
1 |
T |
20 |
2 |
2 |
- |
|
|
|
|
|
|
|
|
C |
= |
3 |
5 |
1 |
C |
3 |
3 |
3 |
- |
|
|
|
|
|
|
|
|
C |
= |
3 |
19 |
1 |
C |
3 |
3 |
3 |
- |
|
|
|
|
|
|
|
|
M |
= |
4 |
10 |
1 |
M |
13 |
4 |
4 |
- |
|
|
- |
|
|
|
|
|
M |
= |
4 |
15 |
1 |
M |
13 |
4 |
4 |
- |
|
|
- |
|
|
|
|
|
N |
= |
5 |
4 |
1 |
N |
14 |
5 |
5 |
- |
|
|
|
|
|
|
|
|
E |
= |
5 |
14 |
1 |
E |
5 |
5 |
5 |
- |
|
|
|
|
|
|
|
|
P |
= |
7 |
1 |
1 |
P |
16 |
7 |
7 |
- |
|
|
|
|
|
|
|
|
P |
= |
7 |
7 |
1 |
P |
16 |
7 |
7 |
- |
|
|
|
|
|
|
|
|
H |
= |
8 |
13 |
1 |
H |
8 |
8 |
8 |
- |
|
|
|
|
|
|
|
|
R |
= |
9 |
2 |
1 |
R |
18 |
9 |
9 |
- |
|
|
- |
|
|
|
|
|
I |
= |
9 |
3 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
|
|
|
I |
= |
9 |
6 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
|
|
|
I |
= |
9 |
8 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
|
|
|
I |
= |
9 |
18 |
1 |
I |
9 |
9 |
9 |
- |
|
|
- |
|
|
|
|
|
|
|
99 |
|
20 |
|
189 |
99 |
99 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
99 |
|
9 |
PRINCIPIA |
95 |
59 |
5 |
|
|
|
|
|
|
|
|
|
- |
- |
9+9 |
- |
11 |
MATHEMATICA |
94 |
40 |
4 |
|
|
|
|
|
1+0 |
1+4 |
|
4+5 |
Q |
- |
18 |
- |
20 |
First Total |
189 |
99 |
9 |
|
|
|
|
|
1 |
5 |
|
9 |
- |
- |
1+8 |
- |
2+0 |
Add to Reduce |
1+8+9 |
9+9 |
- |
|
|
|
|
|
|
|
|
|
Q |
- |
9 |
- |
2 |
Second Total |
18 |
18 |
9 |
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
- |
Reduce to Deduce |
1+8 |
1+8 |
- |
|
|
|
|
|
|
|
|
|
Q |
- |
9 |
- |
2 |
Essence of Number |
9 |
9 |
9 |
|
|
|
|
|
|
|
|
|
9 |
PRINCIPIA |
95 |
59 |
5 |
11 |
MATHEMATICA |
94 |
40 |
4 |
20 |
First Total |
189 |
99 |
9 |
2+0 |
Add to Reduce |
1+8+9 |
9+9 |
- |
2 |
Second Total |
18 |
18 |
9 |
- |
Reduce to Deduce |
1+8 |
1+8 |
- |
2 |
Essence of Number |
9 |
9 |
9 |
|
|
|
|
|
|
|
|
|
|
3 |
3 |
3 |
|
|
|
|
A |
1 |
1 |
1 |
|
|
|
|
|
12 |
3 |
3 |
|
|
|
|
|
3 |
3 |
3 |
|
|
|
|
|
21 |
3 |
3 |
|
|
|
|
|
12 |
3 |
3 |
|
|
|
|
|
21 |
3 |
3 |
|
|
|
|
S |
19 |
10 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9+2 |
2+9 |
2+9 |
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
1+1 |
1+1 |
1+1 |
|
|
|
|
|
|
|
|
|
|
|
|
CURRICULUM |
|
|
- |
|
C |
3 |
3 |
|
|
U |
21 |
3 |
|
|
R |
18 |
9 |
|
|
R |
18 |
9 |
|
|
I |
9 |
9 |
|
|
C |
3 |
3 |
|
|
U |
21 |
3 |
|
|
L |
12 |
3 |
|
|
U |
21 |
3 |
|
|
M |
13 |
4 |
|
10 |
CURRICULUM |
139 |
49 |
49 |
1+0 |
- |
1+3+9 |
4+9 |
4+9 |
1 |
CURRICULUM |
13 |
13 |
13 |
- |
- |
1+3 |
1+3 |
1+3 |
1 |
CURRICULUM |
4 |
4 |
4 |
|
CURRICULUM |
|
|
- |
|
|
|
|
|
C |
3 |
3 |
|
|
3 |
|
|
|
U |
21 |
3 |
|
|
3 |
|
|
|
R |
18 |
9 |
|
|
|
|
9 |
|
R |
18 |
9 |
|
|
|
|
9 |
|
I |
9 |
9 |
|
|
|
|
9 |
|
C |
3 |
3 |
|
|
3 |
|
|
|
U |
21 |
3 |
|
|
3 |
|
|
|
L |
12 |
3 |
|
|
3 |
|
|
|
U |
21 |
3 |
|
|
3 |
|
|
|
M |
13 |
4 |
|
|
|
4 |
|
10 |
CURRICULUM |
139 |
49 |
49 |
|
18 |
4 |
27 |
1+0 |
- |
1+3+9 |
4+9 |
4+9 |
|
1+8 |
- |
2+7 |
1 |
CURRICULUM |
13 |
13 |
13 |
|
9 |
4 |
9 |
- |
- |
1+3 |
1+3 |
1+3 |
|
- |
- |
- |
1 |
CURRICULUM |
4 |
4 |
4 |
|
9 |
4 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4+6 |
|
|
|
9+1 |
4+6 |
4+6 |
|
|
|
|
|
1+0 |
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+0 |
|
|
|
1+0 |
1+0 |
1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4+6 |
|
|
|
9+1 |
4+6 |
4+6 |
|
|
|
|
|
1+0 |
|
|
|
1+8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+0 |
|
|
|
1+0 |
1+0 |
1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
23 |
5 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9+1 |
4+6 |
4+6 |
|
|
|
|
|
1+0 |
|
|
|
3+6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+0 |
1+0 |
1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
1 |
|
18 |
9 |
|
|
|
|
1 |
|
5 |
5 |
|
|
|
|
1 |
|
23 |
5 |
|
|
|
|
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9+1 |
4+6 |
4+6 |
|
1+0 |
3+6 |
|
|
|
|
|
|
|
|
|
|
1+0 |
1+0 |
1+0 |
|
|
|
|
|
|
|
|
|
|
|
ALGEBRA
|
|
|
|
7 |
ALGEBRA |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
1 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
3 |
1 |
L |
12 |
3 |
|
|
|
|
3 |
|
|
|
|
|
|
G |
|
|
7 |
1 |
G |
7 |
7 |
|
|
|
|
|
- |
|
|
|
|
|
E |
|
|
6 |
1 |
E |
5 |
5 |
|
|
|
|
- |
|
|
|
|
|
|
B |
|
|
4 |
1 |
B |
2 |
2 |
|
|
- |
|
|
|
|
|
|
|
|
R |
|
|
5 |
1 |
R |
|
|
|
|
|
- |
|
|
|
|
|
|
|
A |
|
|
1 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
46 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
2+8 |
|
- |
- |
4+6 |
2+8 |
2+8 |
- |
|
|
- |
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
1+0 |
|
- |
- |
1+0 |
1+0 |
1+0 |
- |
|
|
- |
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
1 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
2 |
1 |
L |
12 |
3 |
|
|
|
|
3 |
|
|
|
|
|
|
G |
|
|
3 |
1 |
G |
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
4 |
1 |
E |
5 |
5 |
|
|
|
|
- |
|
|
|
|
|
|
B |
|
|
5 |
1 |
B |
2 |
2 |
|
|
- |
|
|
|
|
|
|
|
|
R |
|
|
6 |
1 |
R |
|
|
|
|
|
- |
|
|
|
|
|
|
|
A |
|
|
7 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
46 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
2+8 |
|
- |
- |
4+6 |
2+8 |
2+8 |
- |
|
|
- |
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
1+0 |
|
- |
- |
1+0 |
1+0 |
1+0 |
- |
|
|
- |
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
1 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
7 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
5 |
1 |
B |
2 |
2 |
|
|
- |
|
|
|
|
|
|
|
|
L |
|
|
2 |
1 |
L |
12 |
3 |
|
|
|
|
3 |
|
|
|
|
|
|
E |
|
|
4 |
1 |
E |
5 |
5 |
|
|
|
|
- |
|
|
|
|
|
|
G |
|
|
3 |
1 |
G |
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
6 |
1 |
R |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
46 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
2+8 |
|
- |
- |
4+6 |
2+8 |
2+8 |
- |
|
|
- |
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
1+0 |
|
- |
- |
1+0 |
1+0 |
1+0 |
- |
|
|
- |
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
|
|
|
|
|
|
|
A |
|
|
1 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
A |
|
|
7 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
B |
|
|
5 |
1 |
B |
2 |
2 |
|
|
- |
|
|
|
|
|
L |
|
|
2 |
1 |
L |
12 |
3 |
|
|
|
|
3 |
|
|
|
E |
|
|
4 |
1 |
E |
5 |
5 |
|
|
|
|
- |
|
|
|
G |
|
|
3 |
1 |
G |
7 |
7 |
|
|
|
|
|
|
|
|
R |
|
|
6 |
1 |
R |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
7 |
ALGEBRA |
46 |
|
|
- |
|
|
|
|
|
|
|
|
2+8 |
|
- |
- |
4+6 |
2+8 |
2+8 |
- |
|
|
- |
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
- |
|
|
|
|
|
|
|
|
1+0 |
|
- |
- |
1+0 |
1+0 |
1+0 |
- |
|
|
- |
|
|
|
|
|
|
|
7 |
ALGEBRA |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
1 |
1 |
E |
5 |
5 |
|
|
|
|
- |
|
|
|
|
|
|
Q |
|
|
2 |
1 |
Q |
17 |
8 |
|
|
|
|
|
- |
|
|
|
|
|
U |
|
|
3 |
1 |
U |
21 |
3 |
|
|
|
|
3 |
|
|
|
|
|
|
A |
|
|
4 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
5 |
1 |
T |
20 |
2 |
|
|
- |
|
|
|
|
|
|
|
|
I |
|
|
6 |
1 |
I |
|
|
|
|
|
- |
|
|
|
|
|
|
|
O |
|
|
7 |
1 |
O |
15 |
6 |
|
|
|
|
|
|
|
6 |
|
|
|
N |
|
|
8 |
1 |
N |
14 |
5 |
|
|
|
|
- |
|
|
|
|
|
|
S |
|
|
9 |
1 |
S |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
121 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
2+8 |
|
- |
- |
1+2+1 |
4+9 |
4+0 |
- |
|
|
- |
|
1+0 |
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
1+0 |
|
- |
- |
- |
1+3 |
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
1 |
1 |
E |
5 |
5 |
|
|
|
|
- |
|
|
|
|
|
|
Q |
|
|
2 |
1 |
Q |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
3 |
1 |
U |
21 |
3 |
|
|
|
|
3 |
|
|
|
|
|
|
A |
|
|
4 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
5 |
1 |
T |
20 |
2 |
|
|
- |
|
|
|
|
|
|
|
|
I |
|
|
6 |
1 |
I |
|
|
|
|
|
- |
|
|
|
|
|
|
|
O |
|
|
7 |
1 |
O |
15 |
6 |
|
|
|
|
|
|
|
6 |
|
|
|
N |
|
|
8 |
1 |
N |
14 |
5 |
|
|
|
|
- |
|
|
|
|
|
|
S |
|
|
9 |
1 |
S |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
121 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
4+0 |
|
- |
- |
1+2+1 |
4+9 |
4+0 |
- |
|
|
- |
|
1+0 |
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
- |
- |
1+3 |
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
4 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
9 |
1 |
S |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
5 |
1 |
T |
20 |
2 |
|
|
- |
|
|
|
|
|
|
|
|
U |
|
|
3 |
1 |
U |
21 |
3 |
|
|
|
|
3 |
|
|
|
|
|
|
E |
|
|
1 |
1 |
E |
5 |
5 |
|
|
|
|
- |
|
|
|
|
|
|
N |
|
|
8 |
1 |
N |
14 |
5 |
|
|
|
|
- |
|
|
|
|
|
|
O |
|
|
7 |
1 |
O |
15 |
6 |
|
|
|
|
|
|
|
6 |
|
|
|
Q |
|
|
2 |
1 |
Q |
17 |
8 |
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
6 |
1 |
I |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
121 |
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
4+0 |
|
- |
- |
1+2+1 |
4+9 |
4+0 |
- |
|
|
- |
|
1+0 |
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
- |
- |
1+3 |
- |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
4 |
1 |
A |
|
1 |
|
|
|
|
|
|
|
|
|
S |
|
|
9 |
1 |
S |
|
10 |
|
|
|
|
|
|
|
|
|
T |
|
|
5 |
1 |
T |
20 |
2 |
|
|
- |
|
|
|
|
|
|
U |
|
|
3 |
1 |
U |
21 |
3 |
|
|
|
|
3 |
|
|
|
|
E |
|
|
1 |
1 |
E |
5 |
5 |
|
|
|
|
- |
|
|
|
|
N |
|
|
8 |
1 |
N |
14 |
5 |
|
|
|
|
- |
|
|
|
|
O |
|
|
7 |
1 |
O |
15 |
6 |
|
|
|
|
|
|
6 |
|
|
Q |
|
|
2 |
1 |
Q |
17 |
8 |
|
|
|
|
|
|
|
|
|
I |
|
|
6 |
1 |
I |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
121 |
|
|
- |
|
|
|
|
|
|
|
|
|
4+0 |
|
- |
- |
1+2+1 |
4+9 |
4+0 |
- |
|
|
- |
1+0 |
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
- |
|
|
|
|
|
|
|
|
|
- |
|
- |
- |
- |
1+3 |
- |
|
|
|
- |
|
|
|
|
|
|
|
|
9 |
EQUATIONS |
|
|
|
- |
|
|
|
|
|
|
|
T |
|
|
6 |
1 |
THE |
|
|
|
E |
|
|
|
1 |
EQUATION |
102 |
|
|
|
|
|
|
|
Add to Reduce |
|
|
|
|
|
- |
|
|
Reduce to Deduce |
1+3+5 |
5+4 |
|
|
|
- |
|
|
Essence of Number |
|
|
|

5 |
NAMES |
52 |
16 |
7 |
2 |
OF |
21 |
12 |
3 |
3 |
GOD |
26 |
17 |
8 |
10 |
First Total |
|
|
|
|
Add to Reduce |
9+9 |
4+5 |
- |
1 |
Second Total |
|
|
|
|
Reduce to Deduce |
1+8 |
- |
- |
1 |
Essence of Number |
|
|
|
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z = 351 = Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z = 126 = Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z = 9 = Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
ABCDEFGH I JKLMNOPQ R STUVWXYZ = 351 = ZYXWVUTS R QPONMLKJ I HGFEDCBA
ABCDEFGH I JKLMNOPQ R STUVWXYZ = 126 = ZYXWVUTS R QPONMLKJ I HGFEDCBA
ABCDEFGH I JKLMNOPQ R STUVWXYZ = 9 = ZYXWVUTS R QPONMLKJ I HGFEDCBA
www.merriam-webster.com/dictionary/algorithm
a procedure for solving a mathematical problem (as of finding the greatest common divisor) in a finite number of steps that frequently involves repetition of an ...
algorithm [ˈælgəˌrɪðəm]
n
1. (Mathematics) a logical arithmetical or computational procedure that if correctly applied ensures the solution of a problem Compare heuristic
2. (Mathematics) Logic Maths a recursive procedure whereby an infinite sequence of terms can be generated Also called algorism
[changed from algorism, through influence of Greek arithmos number]
algorithmic adj
aal·go·rithm (lg-rm)
n.
A step-by-step problem-solving procedure, especially an established, recursive computational procedure for solving a problem in a finite number of steps.
algorithmically adv
algorithm (lg-rthm)
A finite set of unambiguous instructions performed in a prescribed sequence to achieve a goal, especially a mathematical rule or procedure used to compute a desired result. Algorithms are the basis for most computer programming.
Noun 1. algorithm - a precise rule (or set of rules) specifying how to solve some problem
algorithmic program, algorithmic rule
formula, rule - (mathematics) a standard procedure for solving a class of mathematical problems; "he determined the upper bound with Descartes' rule of signs"; "he gave us a general formula for attacking polynomials"
sorting algorithm - an algorithm for sorting a list
stemming algorithm, stemmer - an algorithm for removing inflectional and derivational endings in order to reduce word forms to a common stem algorithm
any methodology for solving a certain kind of problem.
See also: Mathematics
Algorithm
From Wikipedia, the free encyclopedia
Flow chart of an algorithm (Euclid's algorithm) for calculating the greatest common divisor (g.c.d.) of two numbers a and b in locations named A and B. The algorithm proceeds by successive subtractions in two loops: IF the test B ≥ A yields "yes" (or true) (more accurately the number b in location B is greater than or equal to the number a in location A) THEN, the algorithm specifies B ← B − A (meaning the number b − a replaces the old b). Similarly, IF A > B, THEN A ← A − B. The process terminates when (the contents of) B is 0, yielding the g.c.d. in A. (Algorithm derived from Scott 2009:13; symbols and drawing style from Tausworthe 1977).
In mathematics and computer science, an algorithm (i/ˈælɡərɪðəm/) is a step-by-step procedure for calculations. Algorithms are used for calculation, data processing, and automated reasoning.
More precisely, an algorithm is an effective method expressed as a finite list[1] of well-defined instructions[2] for calculating a function.[3] Starting from an initial state and initial input (perhaps empty),[4] the instructions describe a computation that, when executed, will proceed through a finite [5] number of well-defined successive states, eventually producing "output"[6] and terminating at a final ending state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as randomized algorithms, incorporate random input.[7]
Though al-Khwārizmī's algorism referred to the rules of performing arithmetic using Hindu-Arabic numerals and the systematic solution of linear and quadratic equations, a partial formalization of what would become the modern algorithm began with attempts to solve the Entscheidungsproblem (the "decision problem") posed by David Hilbert in 1928. Subsequent formalizations were framed as attempts to define "effective calculability"[8] or "effective method";[9] those formalizations included the Gödel–Herbrand–Kleene recursive functions of 1930, 1934 and 1935, Alonzo Church's lambda calculus of 1936, Emil Post's "Formulation 1" of 1936, and Alan Turing's Turing machines of 1936–7 and 1939. Giving a formal definition of algorithms, corresponding to the intuitive notion, remains a challenging problem.[10]
Informal definition
For a detailed presentation of the various points of view around the definition of "algorithm" see Algorithm characterizations. For examples of simple addition algorithms specified in the detailed manner described in Algorithm characterizations, see Algorithm examples.
While there is no generally accepted formal definition of "algorithm," an informal definition could be "a set of rules that precisely defines a sequence of operations."[11] For some people, a program is only an algorithm if it stops eventually; for others, a program is only an algorithm if it stops before a given number of calculation steps.[12]
A prototypical example of an algorithm is Euclid's algorithm to determine the maximum common divisor of two integers; an example (there are others) is described by the flow chart above and as an example in a later section.
Boolos & Jeffrey (1974, 1999) offer an informal meaning of the word in the following quotation:
No human being can write fast enough, or long enough, or small enough† ( †"smaller and smaller without limit ...you'd be trying to write on molecules, on atoms, on electrons") to list all members of an enumerably infinite set by writing out their names, one after another, in some notation. But humans can do something equally useful, in the case of certain enumerably infinite sets: They can give explicit instructions for determining the nth member of the set, for arbitrary finite n. Such instructions are to be given quite explicitly, in a form in which they could be followed by a computing machine, or by a human who is capable of carrying out only very elementary operations on symbols.[13]
The term "enumerably infinite" means "countable using integers perhaps extending to infinity." Thus, Boolos and Jeffrey are saying that an algorithm implies instructions for a process that "creates" output integers from an arbitrary "input" integer or integers that, in theory, can be chosen from 0 to infinity. Thus an algorithm can be an algebraic equation such as y = m + n—two arbitrary "input variables" m and n that produce an output y. But various authors' attempts to define the notion indicate that the word implies much more than this, something on the order of (for the addition example):
Precise instructions (in language understood by "the computer")[14] for a fast, efficient, "good"[15] process that specifies the "moves" of "the computer" (machine or human, equipped with the necessary internally contained information and capabilities)[16] to find, decode, and then process arbitrary input integers/symbols m and n, symbols + and = ... and "effectively"[17] produce, in a "reasonable" time,[18] output-integer y at a specified place and in a specified format.
The concept of algorithm is also used to define the notion of decidability. That notion is central for explaining how formal systems come into being starting from a small set of axioms and rules. In logic, the time that an algorithm requires to complete cannot be measured, as it is not apparently related with our customary physical dimension. From such uncertainties, that characterize ongoing work, stems the unavailability of a definition of algorithm that suits both concrete (in some sense) and abstract usage of the term.
[edit] Formalization
Algorithms are essential to the way computers process data. Many computer programs contain algorithms that detail the specific instructions a computer should perform (in a specific order) to carry out a specified task, such as calculating employees' paychecks or printing students' report cards. Thus, an algorithm can be considered to be any sequence of operations that can be simulated by a Turing-complete system. Authors who assert this thesis include Minsky (1967), Savage (1987) and Gurevich (2000):
Minsky: "But we will also maintain, with Turing . . . that any procedure which could "naturally" be called effective, can in fact be realized by a (simple) machine. Although this may seem extreme, the arguments . . . in its favor are hard to refute".[19]
Gurevich: "...Turing's informal argument in favor of his thesis justifies a stronger thesis: every algorithm can be simulated by a Turing machine ... according to Savage [1987], an algorithm is a computational process defined by a Turing machine".[20]
Typically, when an algorithm is associated with processing information, data is read from an input source, written to an output device, and/or stored for further processing. Stored data is regarded as part of the internal state of the entity performing the algorithm. In practice, the state is stored in one or more data structures.
For some such computational process, the algorithm must be rigorously defined: specified in the way it applies in all possible circumstances that could arise. That is, any conditional steps must be systematically dealt with, case-by-case; the criteria for each case must be clear (and computable).
Because an algorithm is a precise list of precise steps, the order of computation will always be critical to the functioning of the algorithm. Instructions are usually assumed to be listed explicitly, and are described as starting "from the top" and going "down to the bottom", an idea that is described more formally by flow of control.
So far, this discussion of the formalization of an algorithm has assumed the premises of imperative programming. This is the most common conception, and it attempts to describe a task in discrete, "mechanical" means. Unique to this conception of formalized algorithms is the assignment operation, setting the value of a variable. It derives from the intuition of "memory" as a scratchpad. There is an example below of such an assignment.
For some alternate conceptions of what constitutes an algorithm see functional programming and logic programming.
[edit] Expressing algorithms
Algorithms can be expressed in many kinds of notation, including natural languages, pseudocode, flowcharts, programming languages or control tables (processed by interpreters). Natural language expressions of algorithms tend to be verbose and ambiguous, and are rarely used for complex or technical algorithms. Pseudocode, flowcharts and control tables are structured ways to express algorithms that avoid many of the ambiguities common in natural language statements. Programming languages are primarily intended for expressing algorithms in a form that can be executed by a computer, but are often used as a way to define or document algorithms.
There is a wide variety of representations possible and one can express a given Turing machine program as a sequence of machine tables (see more at finite state machine, state transition table and control table), as flowcharts (see more at state diagram), or as a form of rudimentary machine code or assembly code called "sets of quadruples" (see more at Turing machine).
Representations of algorithms can be classed into three accepted levels of Turing machine description:[21]
1 High-level description:
"...prose to describe an algorithm, ignoring the implementation details. At this level we do not need to mention how the machine manages its tape or head." 2 Implementation description:
"...prose used to define the way the Turing machine uses its head and the way that it stores data on its tape. At this level we do not give details of states or transition function." 3 Formal description:
Most detailed, "lowest level", gives the Turing machine's "state table". For an example of the simple algorithm "Add m+n" described in all three levels see Algorithm examples.
[edit] Implementation
Most algorithms are intended to be implemented as computer programs. However, algorithms are also implemented by other means, such as in a biological neural network (for example, the human brain implementing arithmetic or an insect looking for food), in an electrical circuit, or in a mechanical device.
[edit] Computer algorithms
Flowchart examples of the canonical Böhm-Jacopini structures: the SEQUENCE (rectangles descending the page), the WHILE-DO and the IF-THEN-ELSE. The three structures are made of the primitive conditional GOTO (IF test=true THEN GOTO step xxx) (a diamond), the unconditional GOTO (rectangle), various assignment operators (rectangle), and HALT (rectangle). Nesting of these structures inside assignment-blocks result in complex diagrams (cf Tausworthe 1977:100,114).
In computer systems, an algorithm is basically an instance of logic written in software by software developers to be effective for the intended "target" computer(s), in order for the target machines to produce output from given input (perhaps null).
"Elegant" (compact) programs, "good" (fast) programs : The notion of "simplicity and elegance" appears informally in Knuth and precisely in Chaitin:
Knuth: ". . .we want good algorithms in some loosely defined aesthetic sense. One criterion . . . is the length of time taken to perform the algorithm . . .. Other criteria are adaptability of the algorithm to computers, its simplicity and elegance, etc"[22] Chaitin: " . . . a program is 'elegant,' by which I mean that it's the smallest possible program for producing the output that it does"[23]
Chaitin prefaces his definition with: "I'll show you can't prove that a program is 'elegant'"—such a proof would solve the Halting problem (ibid).
Algorithm versus function computable by an algorithm: For a given function multiple algorithms may exist. This will be true, even without expanding the available instruction set available to the programmer. Rogers observes that "It is . . . important to distinguish between the notion of algorithm, i.e. procedure and the notion of function computable by algorithm, i.e. mapping yielded by procedure. The same function may have several different algorithms".[24]
Unfortunately there may be a tradeoff between goodness (speed) and elegance (compactness)—an elegant program may take more steps to complete a computation than one less elegant. An example of using Euclid's algorithm will be shown below.
Computers (and computors), models of computation: A computer (or human "computor"[25]) is a restricted type of machine, a "discrete deterministic mechanical device"[26] that blindly follows its instructions.[27] Melzak's and Lambek's primitive models[28] reduced this notion to four elements: (i) discrete, distinguishable locations, (ii) discrete, indistinguishable counters[29] (iii) an agent, and (iv) a list of instructions that are effective relative to the capability of the agent.[30]
Minsky describes a more congenial variation of Lambek's "abacus" model in his "Very Simple Bases for Computability".[31] Minsky's machine proceeds sequentially through its five (or six depending on how one counts) instructions unless either a conditional IF–THEN GOTO or an unconditional GOTO changes program flow out of sequence. Besides HALT, Minsky's machine includes three assignment (replacement, substitution)[32] operations: ZERO (e.g. the contents of location replaced by 0: L ← 0), SUCCESSOR (e.g. L ← L+1), and DECREMENT (e.g. L ← L − 1).[33] Rarely will a programmer have to write "code" with such a limited instruction set. But Minsky shows (as do Melzak and Lambek) that his machine is Turing complete with only four general types of instructions: conditional GOTO, unconditional GOTO, assignment/replacement/substitution, and HALT.[34]
Simulation of an algorithm: computer (computor) language: Knuth advises the reader that "the best way to learn an algorithm is to try it . . . immediately take pen and paper and work through an example".[35] But what about a simulation or execution of the real thing? The programmer must translate the algorithm into a language that the simulator/computer/computor can effectively execute. Stone gives an example of this: when computing the roots of a quadratic equation the computor must know how to take a square root. If they don't then for the algorithm to be effective it must provide a set of rules for extracting a square root.[36]
This means that the programmer must know a "language" that is effective relative to the target computing agent (computer/computor).
But what model should be used for the simulation? Van Emde Boas observes "even if we base complexity theory on abstract instead of concrete machines, arbitrariness of the choice of a model remains. It is at this point that the notion of simulation enters".[37] When speed is being measured, the instruction set matters. For example, the subprogram in Euclid's algorithm to compute the remainder would execute much faster if the programmer had a "modulus" (division) instruction available rather than just subtraction (or worse: just Minsky's "decrement").
Structured programming, canonical structures: Per the Church-Turing thesis any algorithm can be computed by a model known to be Turing complete, and per Minsky's demonstrations Turing completeness requires only four instruction types—conditional GOTO, unconditional GOTO, assignment, HALT. Kemeny and Kurtz observe that while "undisciplined" use of unconditional GOTOs and conditional IF-THEN GOTOs can result in "spaghetti code" a programmer can write structured programs using these instructions; on the other hand "it is also possible, and not too hard, to write badly structured programs in a structured language".[38] Tausworthe augments the three Böhm-Jacopini canonical structures:[39] SEQUENCE, IF-THEN-ELSE, and WHILE-DO, with two more: DO-WHILE and CASE.[40] An additional benefit of a structured program will be one that lends itself to proofs of correctness using mathematical induction.[41]
Canonical flowchart symbols[42]: The graphical aide called a flowchart offers a way to describe and document an algorithm (and a computer program of one). Like program flow of a Minsky machine, a flowchart always starts at the top of a page and proceeds down. Its primary symbols are only 4: the directed arrow showing program flow, the rectangle (SEQUENCE, GOTO), the diamond (IF-THEN-ELSE), and the dot (OR-tie). The Böhm-Jacopini canonical structures are made of these primitive shapes. Sub-structures can "nest" in rectangles but only if a single exit occurs from the superstructure. The symbols and their use to build the canonical structures are shown in the diagram.
EVOLVE LOVE EVOLVE
LOVES SOLVE LOVES
EVOLVE LOVE EVOLVE
LOGARITHM
Logarithm - Wikipedia
en.wikipedia.org › wiki › Logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a given number x is the exponent to which another fixed ...
Logarithmic scale · ?Natural logarithm · ?Common logarithm · ?Binary logarithm
Introduction to Logarithms - Math is Fun
www.mathsisfun.com › algebra › logarithms
Introduction to Logarithms. In its simplest form, a logarithm answers the question: How many of one number do we multiply to get another number?
?Working with Exponents · ?Logarithms Can Have Decimals · ?Exponents, Roots
|
|
|
|
|
|
103 |
49 |
49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
|
103 |
49 |
49 |
|
|
|
|
|
|
|
|
|
18 |
|
|
4+9 |
|
1+0 |
|
1+0+3 |
4+9 |
4+9 |
|
|
|
|
|
|
|
|
|
1+8 |
|
|
13 |
|
|
|
4 |
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
1+3 |
|
|
|
|
1+3 |
1+3 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
49 |
49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
|
103 |
49 |
49 |
|
|
|
|
|
|
|
|
|
18 |
|
|
4+9 |
|
1+0 |
|
1+0+3 |
4+9 |
4+9 |
|
|
|
|
|
|
|
|
|
1+8 |
|
|
13 |
|
|
|
4 |
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
1+3 |
|
|
|
|
1+3 |
1+3 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
LOGARITHM
LETTERS TRANSPOSED INTO NUMBER REARRANGED IN NUMERICAL MORDER
|
|
|
|
|
|
103 |
49 |
49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
|
103 |
49 |
49 |
|
|
|
|
|
|
|
|
18 |
|
|
4+9 |
|
1+0 |
|
1+0+3 |
4+9 |
4+9 |
|
|
|
|
|
|
|
|
1+8 |
|
|
13 |
|
|
|
4 |
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
1+3 |
|
|
|
|
1+3 |
1+3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
4 |
4 |
|
|
|
|
|
|
|
|
|
MINUS 5
LOGARITHM
ALGORITHM
A |
= |
1 |
- |
10 |
ALGORITHMS |
|
|
|
A |
= |
1 |
- |
9 |
ALGORITHM |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
L |
= |
3 |
- |
1 |
L |
12 |
3 |
3 |
G |
= |
7 |
- |
1 |
G |
7 |
7 |
7 |
O |
= |
6 |
- |
1 |
O |
15 |
6 |
6 |
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
I |
= |
9 |
- |
1 |
I |
9 |
9 |
9 |
T |
= |
2 |
- |
1 |
T |
20 |
2 |
2 |
H |
= |
8 |
- |
1 |
H |
8 |
8 |
8 |
M |
= |
4 |
- |
1 |
M |
13 |
4 |
4 |
- |
- |
49 |
|
9 |
ALGORITHM |
|
|
|
- |
- |
4+9 |
- |
- |
- |
1+0+3 |
4+9 |
4+9 |
- |
- |
|
- |
9 |
ALGORITHM |
|
|
|
- |
- |
1+3 |
- |
- |
- |
- |
1+3 |
1+3 |
- |
- |
|
- |
9 |
ALGORITHM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
|
103 |
49 |
49 |
|
|
|
|
|
|
|
|
|
18 |
|
|
4+9 |
|
1+0 |
|
1+0+3 |
4+9 |
4+9 |
|
|
|
|
|
|
|
|
|
1+8 |
|
|
13 |
|
|
|
4 |
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
1+3 |
|
|
|
|
1+3 |
1+3 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
ALGORITHM
LETTERS TRANSPOSED INTO NUMBER REARRANGED IN NUMERICAL MORDER
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
|
103 |
49 |
49 |
|
|
|
|
|
|
|
|
|
18 |
|
|
4+9 |
|
1+0 |
|
1+0+3 |
4+9 |
4+9 |
|
|
|
|
|
|
|
|
|
1+8 |
|
|
13 |
|
|
|
4 |
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
1+3 |
|
1+0 |
|
|
1+3 |
1+3 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
MINUS THE 5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
|
103 |
49 |
49 |
|
|
|
|
|
|
|
|
18 |
|
|
4+9 |
|
1+0 |
|
1+0+3 |
4+9 |
4+9 |
|
|
|
|
|
|
|
|
1+8 |
|
|
13 |
|
|
|
4 |
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
1+3 |
|
1+0 |
|
|
1+3 |
1+3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
4 |
4 |
|
|
|
|
|
|
|
|
|
Algorithm - Wikipedia, the free encyclopedia en.wikipedia.org/wiki/Algorithm
In mathematics and computer science, an algorithm is a step-by-step procedure for calculations. Algorithms are used for calculation, data processing, and ...
A |
= |
1 |
- |
9 |
ALGORITHM |
|
|
|
A |
= |
1 |
- |
10 |
ALGORITHMS |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
A |
= |
1 |
|
|
|
|
|
|
- |
- |
- |
- |
1 |
A |
1 |
1 |
1 |
- |
- |
- |
- |
1 |
L |
12 |
3 |
3 |
- |
- |
- |
- |
1 |
G |
7 |
7 |
7 |
- |
- |
- |
- |
1 |
O |
15 |
6 |
6 |
- |
- |
- |
- |
1 |
R |
18 |
9 |
9 |
- |
- |
- |
- |
1 |
I |
9 |
9 |
9 |
- |
- |
- |
- |
1 |
T |
20 |
2 |
2 |
- |
- |
- |
- |
1 |
H |
8 |
8 |
8 |
- |
- |
- |
- |
1 |
M+S |
32 |
14 |
5 |
A |
= |
1 |
|
10 |
|
|
|
|
- |
- |
- |
- |
1+0 |
- |
1+2+2 |
5+9 |
5+0 |
A |
= |
1 |
- |
1 |
ALGORITHMS |
|
|
|
- |
- |
- |
- |
- |
- |
- |
1+4 |
- |
A |
= |
1 |
- |
1 |
ALGORITHMS |
|
|
|
|
10 |
|
|
|
|
R |
I |
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
|
|
|
6 |
|
9 |
|
8 |
|
1 |
|
|
|
2+4 |
|
|
|
|
|
- |
|
|
|
15 |
|
9 |
|
8 |
|
19 |
|
|
|
5+1 |
|
|
|
|
|
10 |
|
|
|
|
R |
I |
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
1 |
3 |
7 |
|
9 |
|
2 |
|
4 |
|
|
|
|
2+6 |
|
|
|
|
|
- |
1 |
12 |
7 |
|
18 |
|
20 |
|
13 |
|
|
|
|
7+1 |
|
|
|
|
|
10 |
|
|
|
|
R |
I |
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
1 |
12 |
7 |
15 |
18 |
9 |
20 |
8 |
13 |
19 |
|
|
|
1+2+2 |
|
|
1+0 |
|
|
- |
1 |
3 |
7 |
6 |
9 |
9 |
2 |
8 |
4 |
1 |
|
|
|
5+0 |
|
|
1+0 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
occurs |
x |
|
= |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
occurs |
x |
|
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
3 |
|
|
|
|
|
|
- |
|
|
|
4 |
|
|
|
|
occurs |
x |
|
= |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
- |
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
occurs |
x |
|
= |
|
|
|
|
|
|
|
- |
|
|
8 |
|
|
|
|
|
occurs |
x |
|
= |
|
|
|
|
|
|
|
|
9 |
- |
|
|
- |
|
|
|
occurs |
x |
|
= |
|
|
10 |
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
1+0 |
|
|
|
|
9 |
|
|
|
|
|
|
|
2+7 |
|
|
1+0 |
|
4+1 |
|
1 |
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
- |
1 |
3 |
7 |
6 |
9 |
9 |
2 |
8 |
4 |
1 |
|
|
|
|
|
- |
- |
|
|
1 |
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
1 |
|
|
A |
= |
1 |
- |
10 |
ALGORITHMS |
|
|
|
A |
= |
1 |
- |
9 |
ALGORITHM |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
L |
= |
3 |
- |
1 |
L |
12 |
3 |
3 |
G |
= |
7 |
- |
1 |
G |
7 |
7 |
7 |
O |
= |
6 |
- |
1 |
O |
15 |
6 |
6 |
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
I |
= |
9 |
- |
1 |
I |
9 |
9 |
9 |
T |
= |
2 |
- |
1 |
T |
20 |
2 |
2 |
H |
= |
8 |
- |
1 |
H |
8 |
8 |
8 |
M |
= |
4 |
- |
1 |
M |
13 |
4 |
4 |
- |
- |
49 |
|
9 |
ALGORITHM |
|
|
|
- |
- |
4+9 |
- |
- |
- |
1+0+3 |
4+9 |
4+9 |
- |
- |
|
- |
9 |
ALGORITHM |
|
|
|
- |
- |
1+3 |
- |
- |
- |
- |
1+3 |
1+3 |
- |
- |
|
- |
9 |
ALGORITHM |
|
|
|
A |
= |
1 |
- |
10 |
ALGORITHMS |
|
|
|
A |
= |
1 |
- |
9 |
ALGORITHM |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
T |
= |
2 |
- |
1 |
T |
20 |
2 |
2 |
L |
= |
3 |
- |
1 |
L |
12 |
3 |
3 |
M |
= |
4 |
- |
1 |
M |
13 |
4 |
4 |
5 |
- |
5 |
- |
- |
5 |
- |
- |
5 |
O |
= |
6 |
- |
1 |
O |
15 |
6 |
6 |
G |
= |
7 |
- |
1 |
G |
7 |
7 |
7 |
H |
= |
8 |
- |
1 |
H |
8 |
8 |
8 |
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
I |
= |
9 |
- |
1 |
I |
9 |
9 |
9 |
- |
- |
49 |
|
9 |
ALGORITHM |
|
|
|
- |
- |
4+9 |
- |
- |
- |
1+0+3 |
4+9 |
4+9 |
- |
- |
|
- |
9 |
ALGORITHM |
|
|
|
- |
- |
1+3 |
- |
- |
- |
- |
1+3 |
1+3 |
- |
- |
|
- |
9 |
ALGORITHM |
|
|
|
A |
= |
1 |
- |
10 |
ALGORITHMS |
|
|
|
A |
= |
1 |
- |
9 |
ALGORITHM |
|
|
|
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
|
|
|
A |
= |
1 |
- |
1 |
A |
1 |
1 |
1 |
L |
= |
3 |
- |
1 |
L |
12 |
3 |
3 |
G |
= |
7 |
- |
1 |
G |
7 |
7 |
7 |
O |
= |
6 |
- |
1 |
O |
15 |
6 |
6 |
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
I |
= |
9 |
- |
1 |
I |
9 |
9 |
9 |
T |
= |
2 |
- |
1 |
T |
20 |
2 |
2 |
H |
= |
8 |
- |
1 |
H |
8 |
8 |
8 |
M |
= |
4 |
- |
1 |
M |
13 |
4 |
4 |
- |
- |
49 |
|
9 |
ALGORITHM |
|
|
|
- |
- |
4+9 |
- |
- |
- |
1+0+3 |
4+9 |
4+9 |
- |
- |
|
- |
9 |
ALGORITHM |
|
|
|
- |
- |
1+3 |
- |
- |
- |
- |
1+3 |
1+3 |
- |
- |
|
- |
9 |
ALGORITHM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
122 |
50 |
50 |
|
|
|
|
|
|
|
|
|
18 |
|
|
5+0 |
|
1+0 |
|
1+2+2 |
5+5 |
5+0 |
|
|
|
|
|
|
|
|
|
1+8 |
|
|
|
|
|
|
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
122 |
50 |
50 |
|
|
|
|
|
|
|
|
18 |
|
|
5+0 |
|
1+0 |
|
1+2+2 |
5+5 |
5+0 |
|
|
|
|
|
|
|
|
1+8 |
|
|
|
|
|
|
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
122 |
50 |
50 |
|
|
|
|
|
|
|
|
|
18 |
|
|
5+0 |
|
1+0 |
|
1+2+2 |
5+5 |
5+0 |
|
|
|
|
|
|
|
|
|
1+8 |
|
|
|
|
|
|
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
20 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
122 |
50 |
50 |
|
|
|
|
|
|
|
|
18 |
|
|
5+0 |
|
1+0 |
|
1+2+2 |
5+5 |
5+0 |
|
|
|
|
|
|
|
|
1+8 |
|
|
|
|
|
|
5 |
5 |
5 |
|
|
|
|
|
|
|
|
|
NUMBER
9
THE SEARCH FOR THE SIGMA CODE
Cecil Balmond 1998
Preface to the New Edition
Page 5
Twelve years ago a little boy entered my imagination as he hopped across the centuries and played with numbers. I began to see how the simple architecture of our decimal system could be constructed in secret ways — not a building project this time but an abstract one. On the surface of our arithmetic countless combinations of numbers take part in tedious and exacting calculations but underneath it all there is pattern, governed by a repeating code of integers. The Sigma Code reduces numbers to a single digit and the illusion of the many is seen to be but the reflection of a few. This is not a book on maths: this is a book for anyone who can carry out simple sums in their heads, and who won't be short-changed knowingly.
When Number 9 first came out I received mail from many who played with numbers. They chased patterns; some had special numbers and even mystical systems. I was tempted to write about numerology but resisted. I wanted to write about the intricacy of what the.. numbers actually do and leave the reader to wonder about the larger irrational that seems to hover around such constructions.
If I were writing this book today the numbers would have featured in a wider context of structuring nature's patterns, and also playing the role of animator in algorithms that create unique architectural forms and shapes. I would also include my previous research into other base systems. But this book was a first step which came from a child-like urge, like playing with building blocks, to build out of our numbers — just the simple 1, 2, 3, up to number 9.
RESEARCH R E SEARCH ER RESEARCH
THE LIGHT IS RISING NOW RISING IS THE LIGHT
NUMBER = 534259 = 1 = 534259 NUMBER
NUMBER = 234559 NUMBER
NUMBER = 534259 = 1 = 534259 NUMBER
NUMBERS = 5342591 = 2 = 5342591 NUMBERS
SBUMNER = 1234559 = SBUMNER
NUMBERS = 5342591 = 2 = 5342591 NUMBERS
- |
- |
- |
- |
Q |
NUMBERS |
- |
Q |
Q |
|
|
|
|
|
|
|
|
|
|
N |
= |
5 |
- |
1 |
N |
14 |
5 |
5 |
|
|
|
|
|
|
6 |
7 |
8 |
|
U |
= |
3 |
- |
1 |
U |
21 |
3 |
3 |
|
|
|
|
|
|
6 |
7 |
8 |
|
M |
= |
4 |
- |
1 |
M |
13 |
4 |
4 |
|
|
|
|
|
|
6 |
7 |
8 |
|
B |
= |
2 |
- |
1 |
B |
2 |
2 |
2 |
|
|
|
|
|
|
6 |
7 |
8 |
|
E |
= |
5 |
- |
1 |
E |
5 |
5 |
5 |
|
|
|
|
|
|
6 |
7 |
8 |
|
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
|
|
|
|
|
|
6 |
7 |
8 |
|
S |
= |
1 |
- |
1 |
S |
19 |
1 |
1 |
|
|
|
|
|
|
6 |
7 |
8 |
|
- |
- |
|
|
7 |
|
|
|
|
|
|
|
|
|
10 |
|
7 |
8 |
|
- |
- |
2+9 |
Q |
- |
Q |
9+2 |
2+9 |
2+9 |
|
|
|
|
|
1+0 |
|
|
|
|
Q |
- |
|
- |
7 |
NUMBERS |
|
|
|
|
|
|
|
|
1 |
|
7 |
8 |
|
- |
- |
1+1 |
Q |
- |
Q |
1+1 |
1+1 |
1+1 |
|
|
|
|
|
|
|
|
|
|
Q |
- |
|
- |
7 |
NUMBERS |
|
|
|
|
|
|
|
|
1 |
|
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
Q |
NUMBERS |
- |
Q |
Q |
|
|
|
|
|
|
|
N |
= |
5 |
- |
1 |
N |
14 |
5 |
5 |
|
|
|
|
|
|
|
U |
= |
3 |
- |
1 |
U |
21 |
3 |
3 |
|
|
|
|
|
|
|
M |
= |
4 |
- |
1 |
M |
13 |
4 |
4 |
|
|
|
|
|
|
|
B |
= |
2 |
- |
1 |
B |
2 |
2 |
2 |
|
|
|
|
|
|
|
E |
= |
5 |
- |
1 |
E |
5 |
5 |
5 |
|
|
|
|
|
|
|
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
|
|
|
|
|
|
|
S |
= |
1 |
- |
1 |
S |
19 |
1 |
1 |
|
|
|
|
|
|
|
- |
- |
|
|
7 |
|
|
|
|
|
|
|
|
|
10 |
|
- |
- |
2+9 |
Q |
- |
Q |
9+2 |
2+9 |
2+9 |
|
|
|
|
|
1+0 |
|
Q |
- |
|
- |
7 |
NUMBERS |
|
|
|
|
|
|
|
|
1 |
|
- |
- |
1+1 |
Q |
- |
Q |
1+1 |
1+1 |
1+1 |
|
|
|
|
|
|
|
Q |
- |
|
- |
7 |
NUMBERS |
|
|
|
|
|
|
|
|
1 |
|
- |
- |
- |
- |
Q |
NUMBERS |
- |
Q |
Q |
|
|
|
|
|
|
|
|
|
|
S |
= |
1 |
- |
1 |
S |
19 |
1 |
1 |
|
|
|
|
|
|
6 |
7 |
8 |
|
B |
= |
2 |
- |
1 |
B |
2 |
2 |
2 |
|
|
|
|
|
|
6 |
7 |
8 |
|
U |
= |
3 |
- |
1 |
U |
21 |
3 |
3 |
|
|
|
|
|
|
6 |
7 |
8 |
|
M |
= |
4 |
- |
1 |
M |
13 |
4 |
4 |
|
|
|
|
|
|
6 |
7 |
8 |
|
N |
= |
5 |
- |
1 |
N |
14 |
5 |
5 |
|
|
|
|
|
|
6 |
7 |
8 |
|
E |
= |
5 |
- |
1 |
E |
5 |
5 |
5 |
|
|
|
|
|
|
6 |
7 |
8 |
|
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
|
|
|
|
|
|
6 |
7 |
8 |
|
- |
- |
|
|
7 |
|
|
|
|
|
|
|
|
|
10 |
|
7 |
8 |
|
- |
- |
2+9 |
Q |
- |
Q |
9+2 |
2+9 |
2+9 |
|
|
|
|
|
1+0 |
|
|
|
|
Q |
- |
|
- |
7 |
NUMBERS |
|
|
|
|
|
|
|
|
1 |
|
7 |
8 |
|
- |
- |
1+1 |
Q |
- |
Q |
1+1 |
1+1 |
1+1 |
|
|
|
|
|
|
|
|
|
|
Q |
- |
|
- |
7 |
NUMBERS |
|
|
|
|
|
|
|
|
1 |
|
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
Q |
NUMBERS |
- |
Q |
Q |
|
|
|
|
|
|
|
S |
= |
1 |
- |
1 |
S |
19 |
1 |
1 |
|
|
|
|
|
|
|
B |
= |
2 |
- |
1 |
B |
2 |
2 |
2 |
|
|
|
|
|
|
|
U |
= |
3 |
- |
1 |
U |
21 |
3 |
3 |
|
|
|
|
|
|
|
M |
= |
4 |
- |
1 |
M |
13 |
4 |
4 |
|
|
|
|
|
|
|
N |
= |
5 |
- |
1 |
N |
14 |
5 |
5 |
|
|
|
|
|
|
|
E |
= |
5 |
- |
1 |
E |
5 |
5 |
5 |
|
|
|
|
|
|
|
R |
= |
9 |
- |
1 |
R |
18 |
9 |
9 |
|
|
|
|
|
|
|
- |
- |
|
|
7 |
|
|
|
|
|
|
|
|
|
10 |
|
- |
- |
2+9 |
Q |
- |
Q |
9+2 |
2+9 |
2+9 |
|
|
|
|
|
1+0 |
|
Q |
- |
|
- |
7 |
NUMBERS |
|
|
|
|
|
|
|
|
1 |
|
- |
- |
1+1 |
Q |
- |
Q |
1+1 |
1+1 |
1+1 |
|
|
|
|
|
|
|
Q |
- |
|
- |
7 |
NUMBERS |
|
|
|
|
|
|
|
|
1 |
|
THE
BALANCING
ONE TWO THREE FOUR
FIVE
NINE EIGHT SEVEN SIX
4 FIVE 42 24 6
1 2 3 4 5 6 7 8 9 9 8 7 6 5 4 3 2 1
15 ONE TWO THREE FOUR 208 82 1
4 FIVE 42 24 6
17 NINE EIGHT SEVEN SIX 208 91 1
1234 5 6789
prime number - Whatis Techtarget
https://whatis.techtarget.com/definition/prime-number
A prime number is a whole number greater than 1 whose only factors are 1 and itself. A factor is a whole numbers that can be divided evenly into another number. The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23 and 29.
Prime number - Wikipedia
https://en.wikipedia.org/wiki/Prime_number
The first 25 prime numbers (all the prime numbers less than 100) are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 (sequence A000040 in the OEIS).
A prime number (or a prime) is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 6 is composite because it is the product of two numbers (2 × 3) that are both smaller than 6. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.
There are infinitely many primes, as demonstrated by Euclid around 300 BC. No known simple formula separates prime numbers from composite numbers. However, the distribution of primes within the natural numbers in the large can be statistically modelled. The first result in that direction is the prime number theorem, proven at the end of the 19th century, which says that the probability of a randomly chosen number being prime is inversely proportional to its number of digits, that is, to its logarithm.
Several historical questions regarding prime numbers are still unsolved. These include Goldbach's conjecture, that every even integer greater than 2 can be expressed as the sum of two primes, and the twin prime conjecture, that there are infinitely many pairs of primes having just one even number between them. Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which relies on the difficulty of factoring large numbers into their prime factors. In abstract algebra, objects that behave in a generalized way like prime numbers include prime elements and prime ideals.
Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. There are several proofs of the theorem.
Prime numbers
www-groups.dcs.st-and.ac.uk/history/HistTopics/Prime_numbers.html
Euclid also showed that if the number 2n - 1 is prime then the number 2n-1(2n - 1) is a perfect number. The mathematician Euler (much later in 1747) was able to ...
Prime numbers
Number theory index History Topics Index
Version for printing
Prime numbers and their properties were first studied extensively by the ancient Greek mathematicians.
The mathematicians of Pythagoras's school (500 BC to 300 BC) were interested in numbers for their mystical and numerological properties. They understood the idea of primality and were interested in perfect and amicable numbers.
A perfect number is one whose proper divisors sum to the number itself. e.g. The number 6 has proper divisors 1, 2 and 3 and 1 + 2 + 3 = 6, 28 has divisors 1, 2, 4, 7 and 14 and 1 + 2 + 4 + 7 + 14 = 28.
A pair of amicable numbers is a pair like 220 and 284 such that the proper divisors of one number sum to the other and vice versa.
You can see more about these numbers in the History topics article Perfect numbers.
By the time Euclid's Elements appeared in about 300 BC, several important results about primes had been proved. In Book IX of the Elements, Euclid proves that there are infinitely many prime numbers. This is one of the first proofs known which uses the method of contradiction to establish a result. Euclid also gives a proof of the Fundamental Theorem of Arithmetic: Every integer can be written as a product of primes in an essentially unique way.
Euclid also showed that if the number 2n - 1 is prime then the number 2n-1(2n - 1) is a perfect number. The mathematician Euler (much later in 1747) was able to show that all even perfect numbers are of this form. It is not known to this day whether there are any odd perfect numbers.
In about 200 BC the Greek Eratosthenes devised an algorithm for calculating primes called the Sieve of Eratosthenes.
There is then a long gap in the history of prime numbers during what is usually called the Dark Ages.
PRIME NUMBERS
P |
= |
2 |
- |
5 |
PRIME |
61 |
34 |
7 |
N |
= |
2 |
- |
7 |
NUMBERS |
92 |
38 |
2 |
- |
- |
17 |
- |
12 |
Add to Reduce |
|
|
9 |
- |
- |
1+7 |
- |
1+2 |
Reduce to Deduce |
1+5+3 |
7+2 |
- |
- |
- |
|
- |
|
Essence of
Number |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
2 |
- |
5 |
PRIME |
61 |
34 |
7 |
|
|
|
|
|
|
|
|
|
|
N |
= |
2 |
- |
7 |
NUMBERS |
92 |
38 |
2 |
|
|
|
|
|
|
|
|
|
|
- |
- |
17 |
- |
12 |
Add to Reduce |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
16 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
11 |
|
61 |
34 |
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
10 |
|
92 |
38 |
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+5 |
|
|
|
2+7 |
P |
= |
2 |
- |
5 |
PRIME |
61 |
34 |
7 |
|
|
|
|
|
|
|
|
|
|
N |
= |
2 |
- |
7 |
NUMBERS |
92 |
38 |
2 |
|
|
|
|
|
|
|
|
|
|
- |
- |
17 |
- |
12 |
Add to Reduce |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+7 |
- |
1+2 |
Reduce to Deduce |
1+5+3 |
7+2 |
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
|
Essence of
Number |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
2 |
- |
5 |
PRIME |
61 |
34 |
7 |
|
|
|
|
|
|
|
|
|
|
N |
= |
2 |
- |
7 |
NUMBERS |
92 |
38 |
2 |
|
|
|
|
|
|
|
|
|
|
- |
- |
17 |
- |
12 |
Add to Reduce |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
16 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+5 |
|
|
|
2+7 |
P |
= |
2 |
- |
5 |
PRIME |
61 |
34 |
7 |
|
|
|
|
|
|
|
|
|
|
N |
= |
2 |
- |
7 |
NUMBERS |
92 |
38 |
2 |
|
|
|
|
|
|
|
|
|
|
- |
- |
17 |
- |
12 |
Add to Reduce |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+7 |
- |
1+2 |
Reduce to Deduce |
1+5+3 |
7+2 |
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
|
Essence of
Number |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
2 |
- |
5 |
PRIME |
61 |
34 |
7 |
|
|
|
|
|
|
|
|
|
|
N |
= |
2 |
- |
7 |
NUMBERS |
92 |
38 |
2 |
|
|
|
|
|
|
|
|
|
|
- |
- |
17 |
- |
12 |
Add to Reduce |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
16 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+5 |
|
|
|
2+7 |
P |
= |
2 |
- |
5 |
PRIME |
61 |
34 |
7 |
|
|
|
|
|
|
|
|
|
|
N |
= |
2 |
- |
7 |
NUMBERS |
92 |
38 |
2 |
|
|
|
|
|
|
|
|
|
|
- |
- |
17 |
- |
12 |
Add to Reduce |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
- |
- |
1+7 |
- |
1+2 |
Reduce to Deduce |
1+5+3 |
7+2 |
- |
|
|
|
|
|
|
|
|
|
|
- |
- |
|
- |
|
Essence of
Number |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 +8 = 14 1+4 = 5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
= |
2 |
- |
5 |
PRIME |
61 |
34 |
7 |
|
|
|
|
|
|
|
|
N |
= |
2 |
- |
7 |
NUMBERS |
92 |
38 |
2 |
|
|
|
|
|
|
|
|
- |
- |
17 |
- |
12 |
Add to Reduce |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
|
19 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
|
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
|
13 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
|
14 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
1 |
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
16 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
1 |
|
18 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+5 |
|
2+7 |
P |
= |
2 |
- |
5 |
PRIME |
61 |
34 |
7 |
|
|
|
|
|
|
|
|
N |
= |
2 |
- |
7 |
NUMBERS |
92 |
38 |
2 |
|
|
|
|
|
|
|
|
- |
- |
17 |
- |
12 |
Add to Reduce |
|
|
9 |
|
|
|
|
|
|
|
|
- |
- |
1+7 |
- |
1+2 |
Reduce to Deduce |
1+5+3 |
7+2 |
- |
|
|
|
|
|
|
|
|
- |
- |
|
- |
|
Essence of
Number |
|
|
|
|
|
|
|
|
|
|
|
I = 9 9 = I
ME = 9 9 = ME
BRAIN + BODY = 9 9 = BODY + BRAIN
LIGHT + DARK = 9 9 = DARK + LIGHT
ENERGY + MASS = 9 9 = MASS +ENERGY
MIND + MATTER = 9 9 = MATTER + MIND
MAGNETIC + FIELD = 9 9 = FIELD + MAGNETIC
POSITIVE + NEGATIVE = 9 9 = NEGATIVE + POSITIVE
973 OM AZAZAZAZAZAZAZAZAZZAZAZAZAZAZAZAZAZAOM 973